|
University of Minnesota School of Mathematics |
|
Bifurcations from an Invariant Circle for Two-Parameter Families of Maps of the Plane: A Computer-Assisted Study D. G. Aronson, M. A. Chory, G. R. Hall, & R. P. McGehee Comm. Math. Phys. 3 (1982), 304-354. doi:10.1007/BF01213607
|
| School of Mathematics | |||
| Richard McGehee | |||
| Aronson et al. 1982 | |||
Abstract.
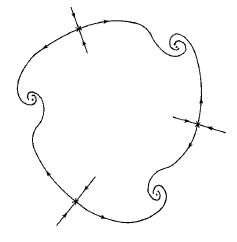
We consider a two-parameter family of maps of the plane to itself. Each map has a fixed
point in the first quadrant and is a diffeomorphism in a neighborhood of this point. For
certain parameter values there is a Hopf bifurcation to an invariant circle, which is
smooth for parameter values in a neighborhood of the bifurcation point. However, computer
simulations show that the corresponding invariant set fails to be even topologically a
circle for parameter values far from the bifurcation point. This paper is an attempt to
elucidate some of the mechanisms involved in this loss of smoothness and alteration of
topological type. |
Electronic Copies Reprints are available for download to subscribers from the journal website:
|