| University of Minnesota School of Mathematics |
|
Arnold Flames and Resonance Surface Folds Richard P. McGehee and Bruce B. Peckham International Journal of Bifurcation and Chaos 6 (1996), 315-336. doi:10.1142/S0218127496000072 |
| School of Mathematics | |||
| Richard McGehee | |||
| McGehee & Peckham 1996 | |||
| Preprint | |||
| Figures | |||
Abstract. Periodically forced planar oscillators are often studied by varying the
two parameters of forcing amplitude and forcing frequency.
For low forcing amplitudes, the study of the essential oscillator dynamics
can be reduced to the study of families of circle maps.
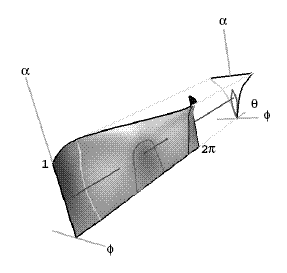
The primary features of the resulting parameter plane bifurcation
diagrams are "(Arnold) resonance horns" emanating from zero forcing amplitude.
Each horn is characterized by the existence of a periodic orbit with a certain
period and
rotation number. In this paper we investigate divisions of these horns
into subregions -- different subregions corresponding to maps having
different numbers
of periodic orbits. The existence of subregions having more than the
"usual" one pair of attracting and repelling periodic
orbits implies the existence of "extra folds" in the
corresponding surface of periodic points in the cartesian product of the
phase and parameter spaces.
The existence of more than one attracting and one repelling periodic orbit
is shown to be generic.
For some of the families we create, the resulting parameter plane bifurcation
pictures appear in shapes we call "Arnold flames."
Results apply both to circle maps and forced oscillator maps.
|
Electronic Copies Reprints are available to subscribers for download from the journal Web site: The original preprint was posted on July 27, 1995, at the Geometry Center as GCG 84.
The Geometry Center Website is maintained now at the University of Illinois. Preprint Text (cached pdf file) |