Classification of critical sets and their images for quadratic maps of the plane
Chia-Hsing Nien, Bruce B. Peckham, and Richard P. McGehee
Journal of Difference Equations and Applications 22 (5) (2016) 637-655. doi: 10.1080/10236198.2015.1127360
| School of Mathematics | |||||||||
| Richard McGehee | |||||||||
| |||||||||
|
Abstract.
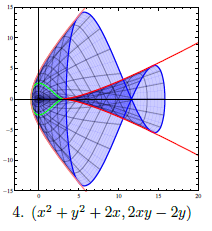
We provide a complete classification of the critical sets and their images
for quadratic maps of the real plane. Critical sets are always conic sections,
which provides a starting point for the classification. The generic cases,
maps whose critical sets are either ellipses or hyperbolas, was published
by Delgado et al. in 2013. This work completes the classification by including
all the nongeneric cases: the empty set, a single point, a single line, a
parabola, two parallel lines, two intersecting lines, or the whole plane.
We describe all possible images for each critical set case and illustrate
the geometry of representative maps for each case. |
|
Electronic Copies The paper is available for subscribers on the publisher's Web site: A preprint was posted on ArXiv on 9 July 2015: |