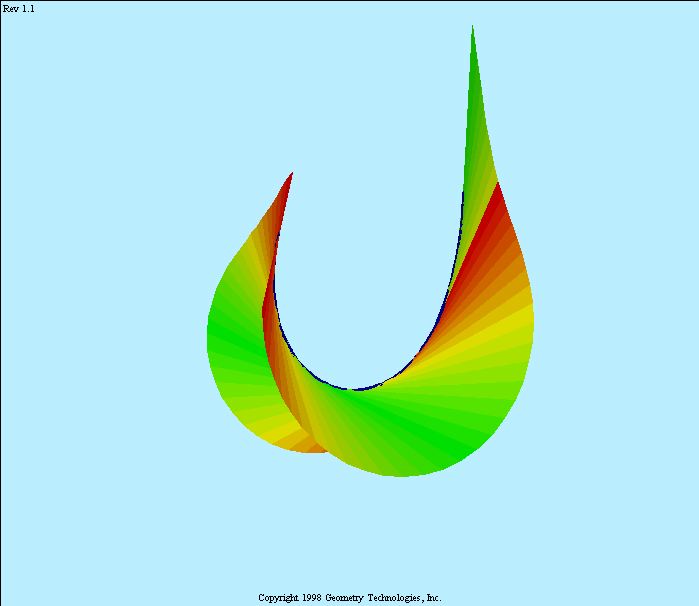
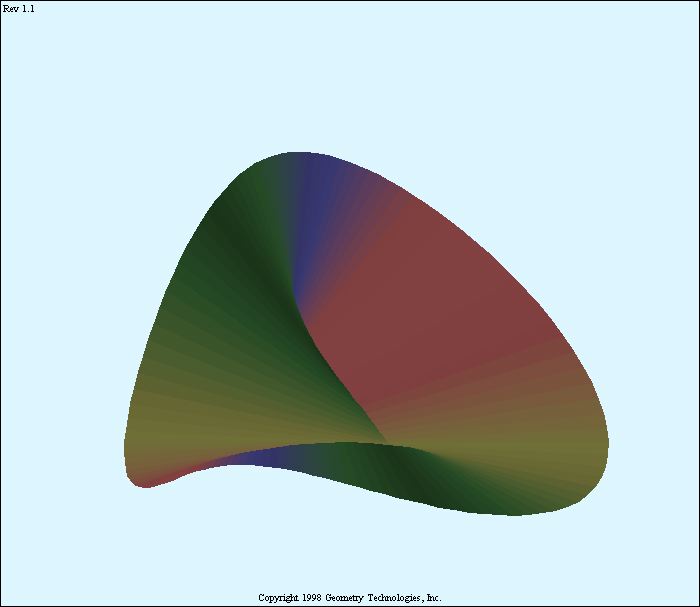
- Plane curves of degree 2 are called conics;
curves of degree 3 are called cubics. -
Standard conics:
ellipse, parabola,
and hyperbola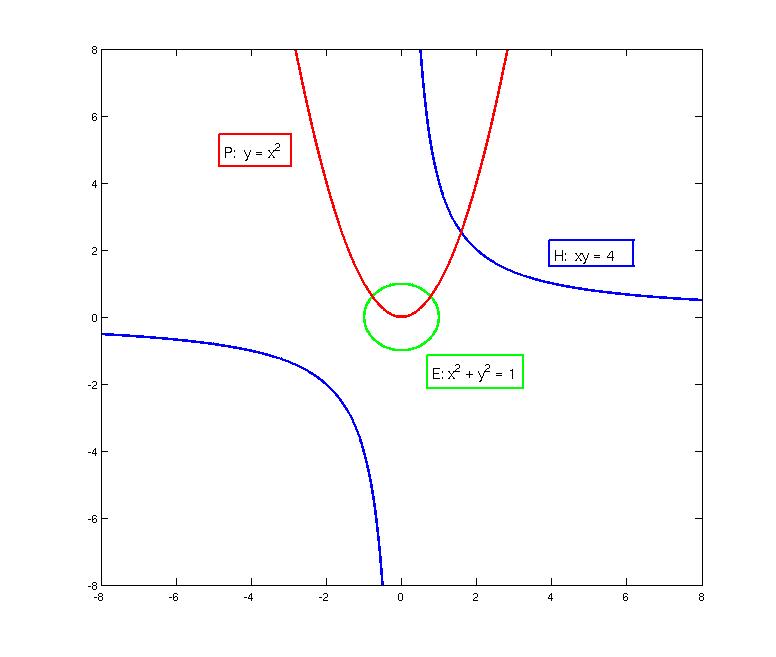
Projective closures
and the line
at infinity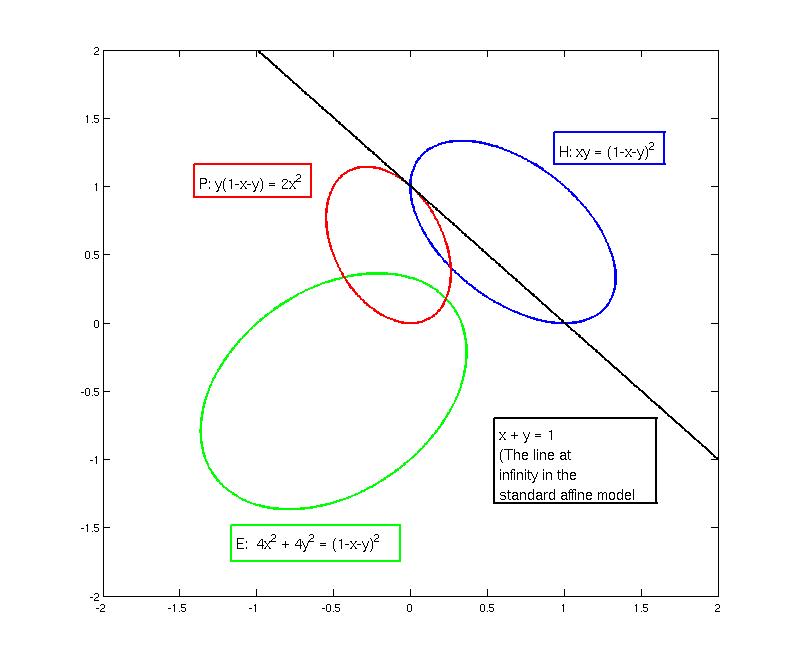
A family of cubics

- The hyperbola is disconnected because its projective closure intersects
the line at infinity twice.
- { The real projective plane
consists of Euclidean plane R² and a "line" of points of
infinity. There is one point at infinity for each class of parallel lines
in R². }
- { The real projective plane
consists of Euclidean plane R² and a "line" of points of
infinity. There is one point at infinity for each class of parallel lines
in R². }
- Some of the real cubics, however, have the property that their projective
closures are disconnected.
- More generally, the projective closure of the real curve
y² = f(x) has connected components
that correspond to the intervals where
f(x) > 0.
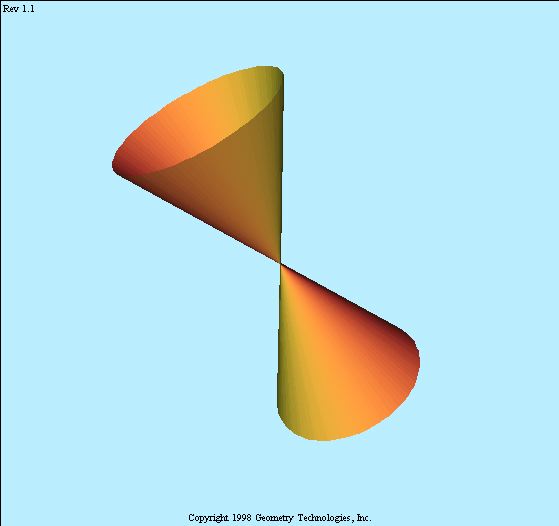
Quadric surfaces, mostly ruled ones
|
|
|
|
|
- The quadric cone has a unique singular point, namely its vertex.
- {
A singular point of the surface
f(x,y,z) = 0 is a point of the surface
where ∂f/∂x(x,y,z) = ∂f/∂y(x,y,z) = ∂f/∂z(x,y,z) = 0. }
- {
A singular point of the surface
f(x,y,z) = 0 is a point of the surface
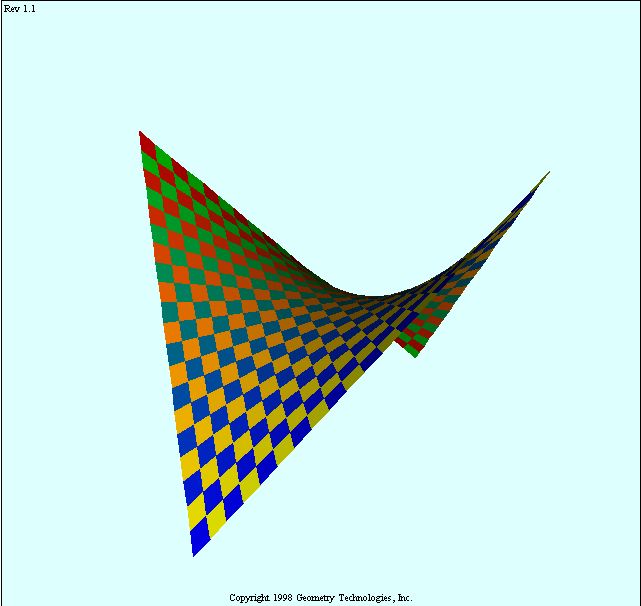
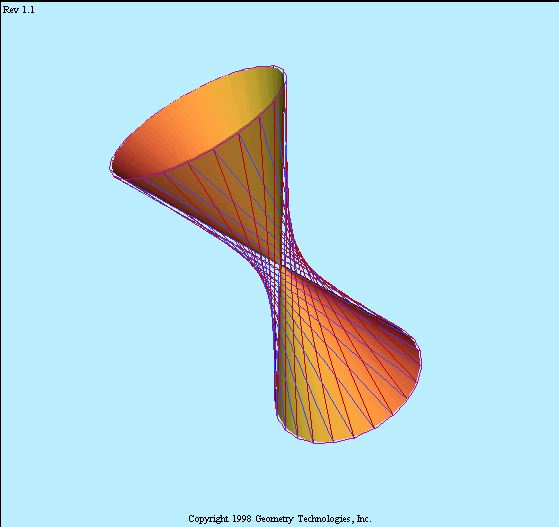
- Each of the smooth quadric ruled surfaces contains
two families of straight lines.
- The intersection of the hyperboloid and the tangent plane is a
reducible plane conic
-- accordingly, the union of two lines in the tangent plane.
- Every smooth quadric over C is ruled.
- Non-ruled smooth (real) quadrics: ellipsoid,
elliptic paraboloid, hyperboloid of two sheets.
- Sketches not currently available
- The intersection of each surface with a tangent plane is a (singular) conic with only one real point.
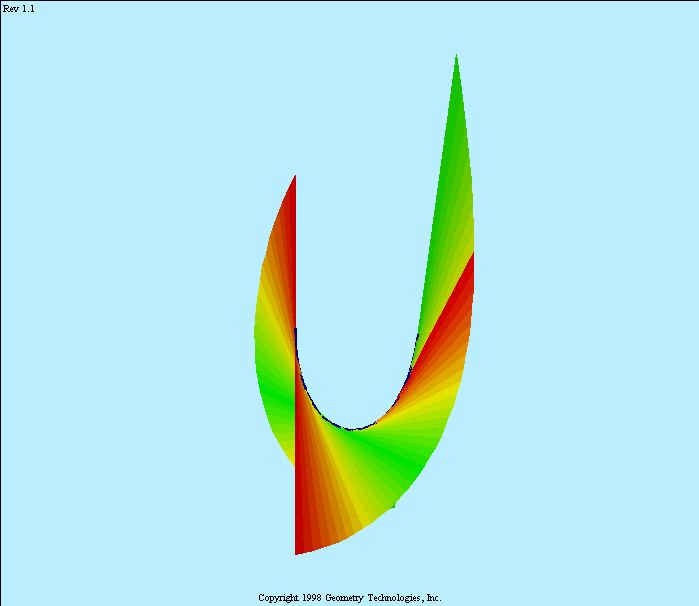
Tangent surfaces of space curves.
|
|
- The tangent surface of a curve is singular at all points of the curve itself.
|
|
Images under generic projection.
|
|
In the neighborhood of a singular point, the local dimension of a real variety can be lower than what you might expect.
Projective duality
- For a smooth surface X in P³, the dual variety
parametrizes the set of tangent planes of X. For a non-smooth
surface, we work with the closure of the set of tangent planes at smooth
points.
-
The Cayley Surface 
- The Cayley surface is dual to the Steiner surface.
- Some static pictures of the Cayley surface.
- A picture from
Bernd Sturmfels' IMA workshop lecture
in January 2007
-
http://www.mathcurve.com/surfaces/cayley/cayley.shtml
(Robert Férreol and Alain Esculier)
-
http://surf.sourceforge.net/gallery/cayley.jpg (Surf)
- A picture from
Bernd Sturmfels' IMA workshop lecture
in January 2007
About the pictures
- Please
don'tdo this at home.
- Actually I feel very strongly that it's more beneficial to
actively view
the surface pictures by rotating them with the mouse, rather than just
looking at the view that I've chosen to present.
- Actually I feel very strongly that it's more beneficial to
actively view
- The Geometry Center and JGV
- The Geometry Center existed at the University of Minnesota prior to
1998; it was funded by the National Science Foundation. Although it is
now closed, its webpages still exist and are hosted by the University of
Illinois. Here is the current URL:
http://geom.math.uiuc.edu/
- The Java GeomView software was developed at the Geometry Center.
You don't need this software for viewing my pages. If, however, you'd
like to obtain it for your own webpage, you can download it from the
following URL:
http://geom.math.uiuc.edu/java/JGV/
- The Geometry Center existed at the University of Minnesota prior to
1998; it was funded by the National Science Foundation. Although it is
now closed, its webpages still exist and are hosted by the University of
Illinois. Here is the current URL:
- About Java
- When you view one of these figures, your computer downloads the Java
applet (a small application) from the U of MN math department
web server, along with the surface coordinates and related data from my
web page. When you rotate, translate, or scale the figure by dragging it
with your computer's mouse, the computations are done on your
computer in real time. Thus, you don't have to wait for the server
to re-draw the figure.
- When you view one of these figures, your computer downloads the Java
applet (a small application) from the U of MN math department
web server, along with the surface coordinates and related data from my
web page. When you rotate, translate, or scale the figure by dragging it
with your computer's mouse, the computations are done on your
computer in real time. Thus, you don't have to wait for the server
to re-draw the figure.
- "Triangulation" vs. ray tracing.
- Although the term "triangulation" is commonly used by computer
graphics people, we're not generally referring to triangles,
but rather to other polygonal figures that we use to approximate
surfaces. Quadrilaterals are very common; for example that is
what you'd have with a parametric sketch
created in Matlab, Maple, or Mathematica. And we're often not looking
at actual planar polygons. But this turns out not to matter!!
Indeed, the edges of our polygon approximate curve segments on the
surface. These are projected onto the plane of the computer screen,
finally giving an actual polygon. This is finally filled in with whatever
color is given in my webpage data.
- If we use a grid with relatively few vertices to plot our surface,
we may get a picture that's not as smooth as what can be done by tools such
as surf. But, as mentioned above,
we are able to take advantage of the cross-platform capabilities of the
Java language, thereby obtaining figures that can be rotated much more
readily.
- Although the term "triangulation" is commonly used by computer
graphics people, we're not generally referring to triangles,
but rather to other polygonal figures that we use to approximate
surfaces. Quadrilaterals are very common; for example that is
what you'd have with a parametric sketch
created in Matlab, Maple, or Mathematica. And we're often not looking
at actual planar polygons. But this turns out not to matter!!
Indeed, the edges of our polygon approximate curve segments on the
surface. These are projected onto the plane of the computer screen,
finally giving an actual polygon. This is finally filled in with whatever
color is given in my webpage data.