- Examples and properties of plane curves
- Quadric surfaces, mostly ruled ones
- Tangent surfaces and their singularities
- Generic projections
- Projective duality
- About the pictures
- Please
don'tdo this at home.- Actually I feel very strongly that it's more beneficial to
actively view
the surface pictures by rotating them with the mouse, rather than just
looking at the view that I've chosen to present.
- Actually I feel very strongly that it's more beneficial to
actively view
- The Geometry Center and JGV
- About Java
- "Triangulation" vs. . . .
- Please
Examples and properties of plane curves
Quadric surfaces, mostly ruled ones Tangent surfaces of space curves.
Images under generic projection.
Standard conics:
ellipse, parabola,
and hyperbola
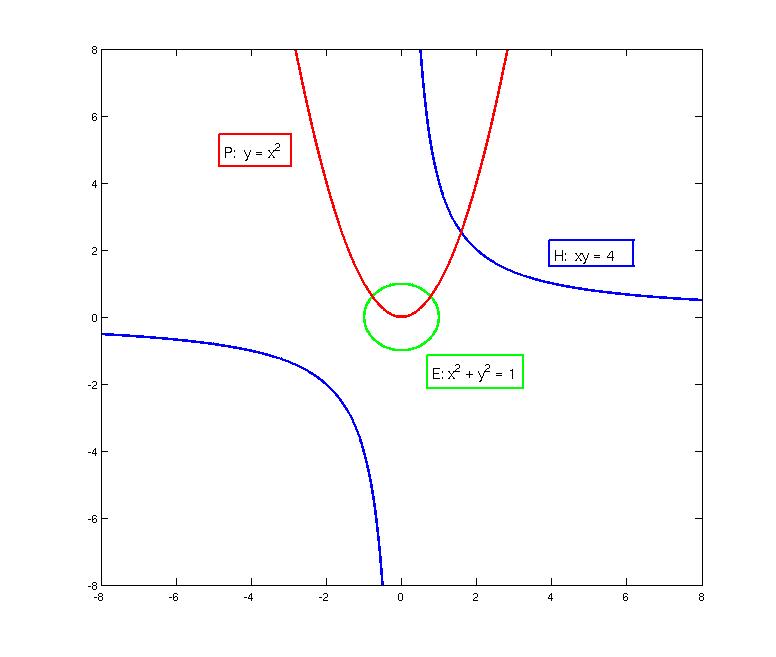
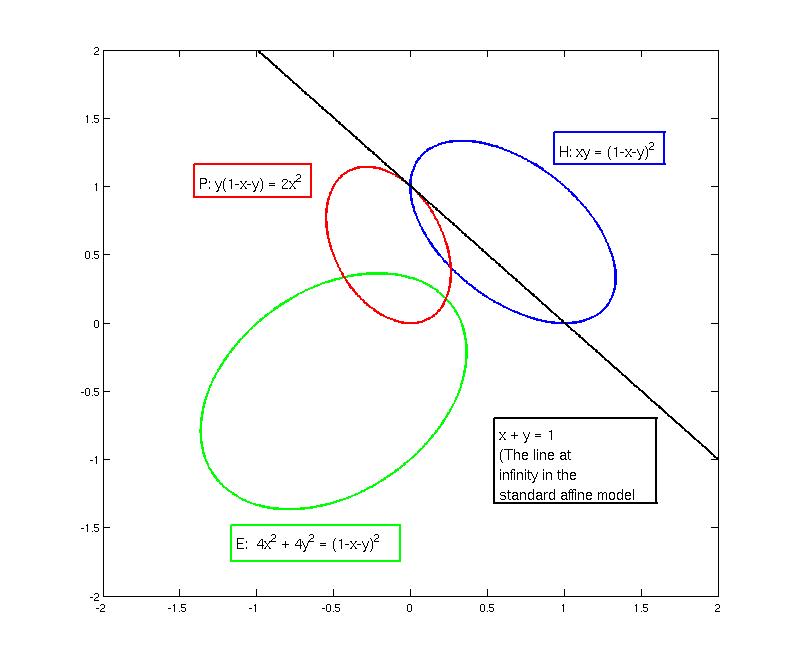
Projective closures
and the line
at infinity
A family of cubics

that correspond to the intervals where
f(x) > 0.
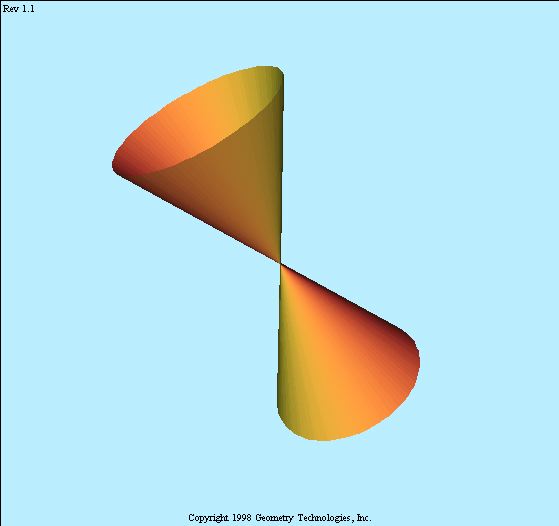
Quadric cone
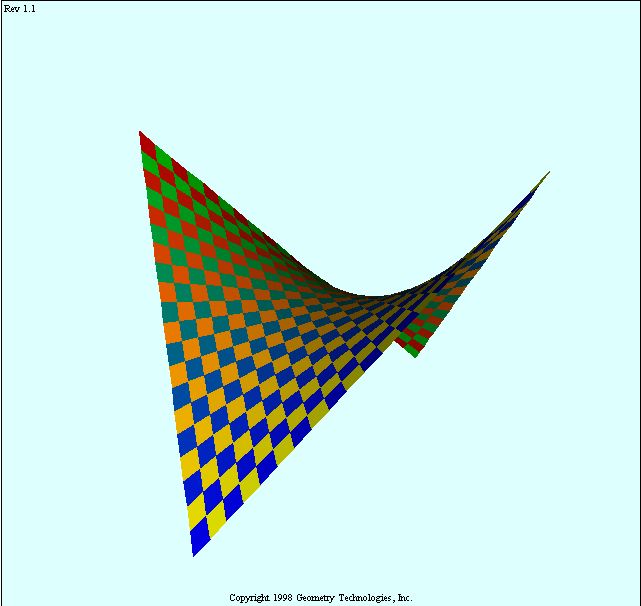
Hyperbolic paraboloid
Hyperboloid of one sheet

A cone asymptotic to a hyperboloid
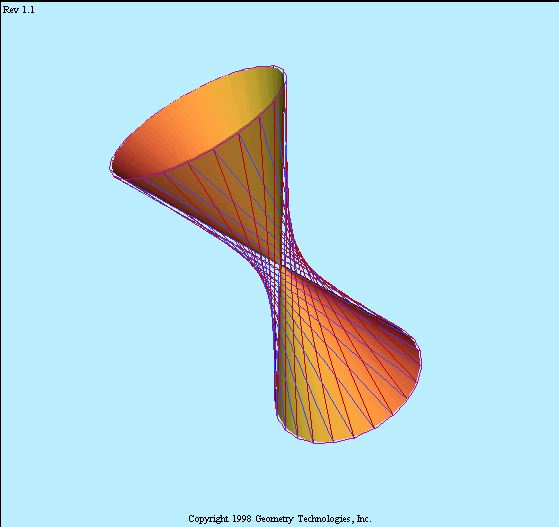
The hyperboloid and a tangent plane

-- accordingly, the union of two lines in the tangent plane.
The image of a
rectangular coordinate patch
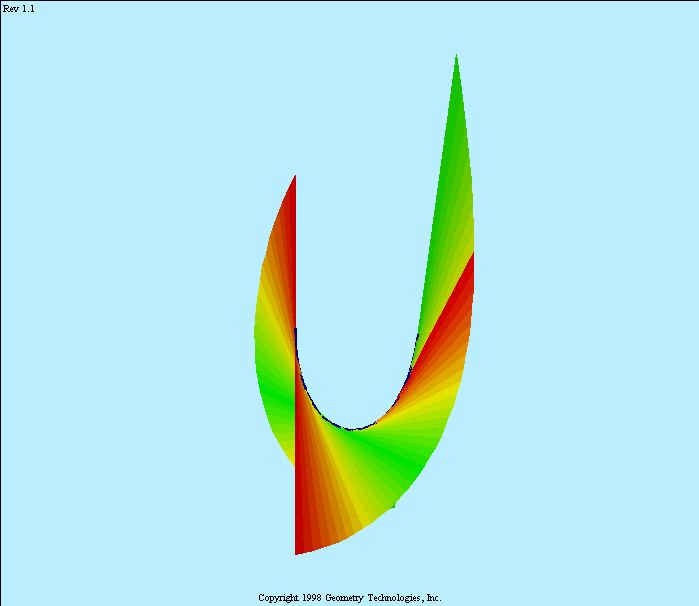
Another view, with
equal length tangent line segments
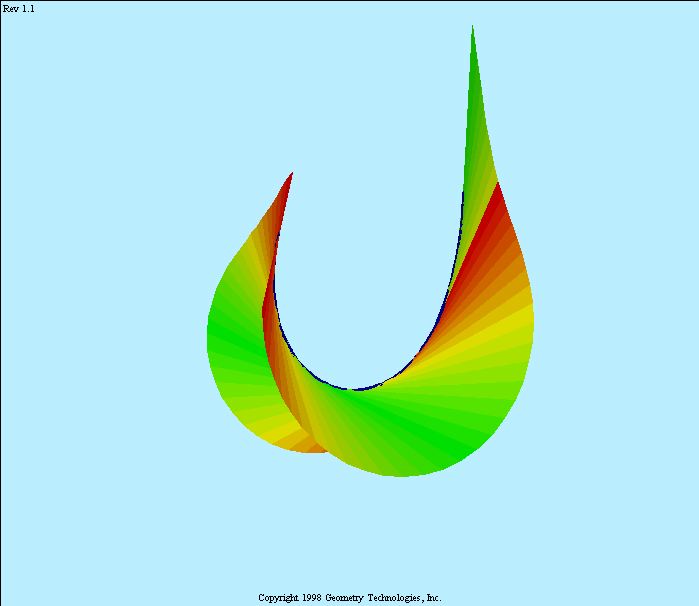
Hence, these surfaces can have other components of their singular loci
that resemble the ordinary double points of a generic projection.
Cubic ruled surface
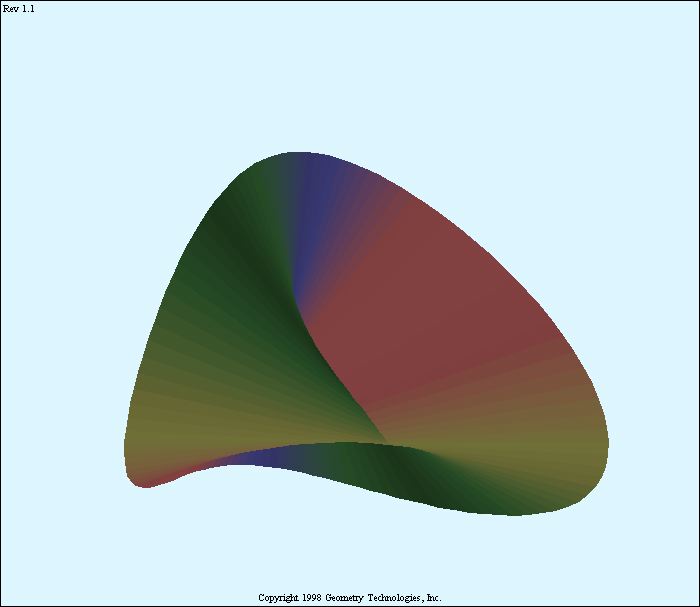
The Steiner surface

 X to
Pn
X to
Pn Pn.}
Pn.}
In the neighborhood of a singular point, the local dimension
of a real variety can be lower than what you might expect.
Projective duality
About the pictures
don't do this at home.
the surface pictures by rotating them with
the mouse, rather than just
looking at the view that I've
chosen to present.
http://geom.math.uiuc.edu/
http://geom.math.uiuc.edu/java/JGV/