Math 3113, Section 4

Fall 1999

Suggestions for exercises 4.3.9 and 4.3.10
  1. Here are some questions that may help you get started.
    1. How many faces does a tree have?
    2. To count the edges of the infinite (or exterior) face, consider the following picture. Think of going around its boundary according to the arrows.
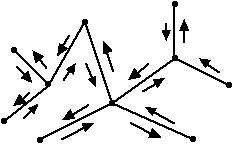
      • How many edges are there in the tree that is shown?
      • How many edges did you count for the exterior face in that tree? In other words, what is the degree of the exterior face?
      • In general, if the number of edges is E, how many edges will we count for the exterior face?
    3. Think of building a general graph by starting with a tree and adding edges to it. In particular, consider the following picture:
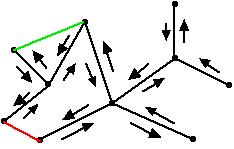
      1. When we add the green edge, what happens to
        • The value of 2E
        • The total of the degrees of the faces. (This will take a bit longer to figure out, since there's now an additional edge.
      2. Answer the same two questions if we now add the red edge.
      3. Try to figure out what happens in general to the following quantities when we add an edge:
        • The value of 2E
        • The sum of the face degrees. (This requires a bit more explaining.)

        Back to the syllabus.