• Exercise 2.1.3(Double letter license plates and double number license plates) This was a class exercise, but it's being presented as background for exercise 2.1.4, a homework exercise which was more confusing.
• Double letters (including triples). According to the exercise, a double letter is where two adjacentletters are the same; but we also have to include the possibility of triple letters. And, presumably, the same applies for double numbers. So, we have these possibilities, where "S" stands for "same" and "D" stands for "different ":
• SSD### 26·1·25·10·10·10 = 650,000possibilities
• DSS### 26·25·1·10·10·10 = 650,000possibilities
• SSS### 26·1·1·10·10·10 = 26,000 possibilities
   
So, altogether there are 650,000 + 650,000 + 26,000 = 1,326,000 possibilities for a license plate with a double letter.
 
• Double numbers (again, including triples) Here, the possibilities for the letters will always be 26·26·26 = 17,576. Combining these with the possibilities for the numbers, we get the following:
• First 2 numbers the same: 26·26·26·10·1·9 = 1,581,840 possibilities
• 2^nd and 3^rd numbers the same: 26·26·26·10·9·1 = 1,581,840 possibilities
• Triple number: 26·26·26·10·1·1 = 175,760 possibilities
   
Altogether, there are 1,581,840 + 1,581,840 + 175,760 = 3,339,440 possibilities for a license plate with a double number.
 

 


• Exercise 2.1.4(License plates which have double letters and/or double numbers)
• Double letter anda double number. Since the question involves "and",we use the multiplication principle. Using "S" for "same" and "D" for "different" in the letters, and #s and #d for "same" and "different" among the numbers, we have these possibilities:
• SSD#s#s#d: 26·1·25·10·1·9 = 58,500 possibilities
• SSD#s#d#d: 26·1·25·10·9·1 = 58,500 possibilities
• DSS#s#s#d: 26·25·1·10·1·9 = 58,500 possibilities
• DSS#d#s#s: 26·25·1·10·9·1 = 58,500 possibilities
• SSS#s#s#d: 26·1·1·10·1·9 = 2,340 possibilities
• SSS#s#s#d: 26·1·1·10·9·1 = 2,340 possibilities
• SSD#s#s#s: 26·1·25·10·1·1 = 6,500 possibilities
• DSS#s#s#s: 26·25·1·10·1·1 = 6,500 possibilities
• SSS#s#s#s: 26·1·1·10·1·1 = 260 possibilities
   
Finally (gasp!), that seems to be everything. Adding all of these numbers, we see that there are 251,940 possibilities for a license plate with a double letter anda double number.
 
• Double letter ora double number Here, the question involves "or", so that we can use the addition principle. The following is a kind of "shortcut". Namely, let's use the formula: n(A B) = n(A) + n(B) - n(A B), from page 31 of the notes. We take:
• A = {all license plates with a double letter}, and
• B = {all license plates with a double number}. Therefore:
• A B = {all license plates with a double letter ora double number}, and
• A B = {all license plates with a double letter anda double number}.
   
So, the expression n(A) + n(B), i.e.simple addition would count the license plates with a double letter anda double number twice. But the formula corrects for this by subtracting off the double count. Thus:n(A B) = n(A) + n(B) - n(A B), or:
n(A B) = 1,326,000 + 3,339,440 - 251,940 = 4,413,500 possibilities for a license plate with a double letter ora double number.

   
• Exercise 2.3.31 [A class exercise] (Choosing 4 students from a group of 10, and then choosing a chairperson, vice chairperson, secretary, and treasurer from these four.)
• There are 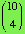  ways to choose a selection of 4 students from a group of 10.
• For each selection of 4, there are 4! ways to arrange them in an ordered list.
• Hence, there are 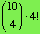 ways in which this process can be done.
• Exercise 2.3.32 [A class exercise] (Choosing a chairperson, vice chairperson, secretary, and treasurer from a group of 10 students).
• There are 10 choices for the chairperson. For each choice of chairperson, there are 9 choices for the vice chairperson. (Etc. …)
• So, the result is that there are (10)₄ = 10·9·8·7 ways to do this process.
• Exercise 2.3.33 [A class exercise] (A formula for  . )
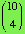• The first step is to observe that there are the same number of possibilities for the process described in exercise 31 as for the process described in exercise 32. Thus, there are exactly as many ways to name a slate of 4 officers and then assign roles as there are ways to elect the 4 officers in a step-by-step process.
• So, we set the two answers equal, getting the following equation:
   

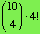     = 10·9·8·7.
 
• We solve this equation, thus finding the formula:
   

   
.  
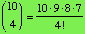
• Exercise 2.3.34 [A homework problem] (Formulas for  . )
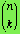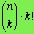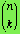• As suggested in the notes, we use exercise 33 (above) as a model. So, (n)_k , the number of permutations of nthings taken kat a time can be given as (i) one of the formulas from §2.2 and (ii) also as  . (In the second viewpoint, there are  ways to choose a subset of kelements, and then k!ways to arrange its elements.)
   
• From exercise 2.2.6, we have the formula (n)_k = n·(n-1)·(n-2)···(n - k+1). We again set the two answers equal, obtaining the following equation:
   

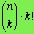     = n·(n-1)·(n-2)···(n - k+1).
 
• We solve this equation, thus finding the formula:
   

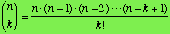      .    (Version 1)
 
• To derive the other version of the formula, we can multiply numerator and denominator of the last fraction by (n-k)!. Thus:
   

      .
 
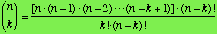{Probably, you could say that the factor (n-k)! was chosen by "working back from the answer", but after doing that to guess the answer, we can see that the algebra is valid.} We handle the numerator in the new fraction by noting that:
 
[n·(n-1)·(n-2)···(n-k+1)]·(n-k)! = [n·(n-1)···(n-k+1)]·(n-k)·(n-k-1)···2·1,
 
which is just n ! So, we can rewrite this formula as:
 
     .     (Version 2)

For questions roberts@math.umn.edu

Back to the syllabus.

Back to the class homepage.