NOTE: It is also strongly recommended to review past homework problems and your notes from group work in class. It is not claimed that the problems on this page represent every type of question that could occur on the test.

1. Area codes for telephone numbers obey the following rules: (I) the first number cannot be 0 or 1; (ii) the second and third numbers can be any number from 0 through 9, but (iii) the second and third numbers cannot be the same.

Determine the number of possible area codes.
Solution: 8·10·9 = 720
 
2. With the same rules as in the previous problem:
1. Determine how many area codes have the first digit equal to 6.

Solution: 1·10·9 = 90
2. Determine how many area codes have the last digit equal to 6.

Solution: 8·10·1 = 80
 
3. Determine how many area codes have the first digit and the last digit equal to 6.

Solution: 1·10·1 = 10
 
4. Determine how many area codes have the first digit or the last digit equal to 6.
• Suggestion: You may be able to use the formula n(AB) = n(A) + n(B) - n(AB).

Solution: If we use the suggestion, then it becomes 90 + 80 - 10 = 160.
Thus, we take A = {area codes with first digit = 6} and B = {area codes with last digit = 6}.
So, AB = {area codes with first and last digits = 6},
while AB = {area codes with first digit = 6 or last digit = 6}
 
3. How many ways can 5 children be chosen from a group of 12 and arranged in a row?
   Solution: We can view it as (12)₅ = 12·11·10·9·8 or as 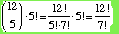 In either case, the numerical value is 95040.

 
4. How many ways can 5 children be arranged in a circle? (Two arrangements are different if some child has a different person the left or a different person on the right.)

Solution: We can choose one child's place in the circle, and then arrange the other children in the remaining 4 places.
There are 4! = 24 ways to do this.
 
5. How many ways can 5 children be chosen from a group of 12 and arranged in a circle.
• Suggestion: Think of this as a process with two steps. The two steps may involve methods from different sections of the notes!

Solution: There are 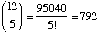 ways to choose 5 children from a group of 12.
For each group, there are 4! = 24 ways to arrange them in a circle.
So, there are 792·24 = 19008 ways to accomplish the assigned task.
 
6. Suppose that Bill lives k blocks south and n-k blocks west from work.

Explain why the number of possible routes Bill can take to work is .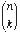
Solution: Bill has to walk nblocks to work: kblocks north and n-kblocks east. Choosing a route is the same as making a "word" of nletters, of which kare N's and n-kare E's. So, we have to choose kof the npositions in which to put the N's. The number of ways to do this is.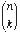
7. = Exercise 2.3.11 in the notes.

Method 1: A set with nelements has a total of 2ⁿ subsets. For each value of kbetween 0 and n(inclusive) there are 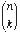 subsets with k elements. This gives the equation:
2ⁿ =  +  +  + ... +  +  +  .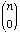
 
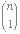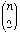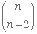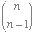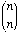Method 2: Apply the binomial theorem with xand yboth equal to 1, to obtain the same equation.
 
8. Use the binomial theorem to evaluate the following:
1. (x - y)⁵

Solution: x⁵ - 5x⁴y +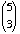x³y² - 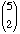x²y³ + 5xy⁴ - y⁵,
or     x⁵ - 5x⁴y + 10x³y² - 10x²y³ + 5xy⁴ - y⁵
 .
2. (3x + y)⁴

  Solution: 3⁴x⁴ + 4·3³x³y + ·3²x²y² + 4·3xy³ + y⁴,
or      81x⁴ + 108x³y + 54x²y² + 12xy³ + y⁴
 
9. = Exercise 2.3.39 in the notes.

Solution: I think that choosing a team is just supposed to mean that we choose the members of the team, rather than assigning them to particular positions.
So, this can be done in 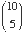 ways.
10. = Exercise 2.3.40 in the notes.

Solution: I had thought that this was the same as the previous problem, but one member of the class pointed out another interpretation. Namely, we can completely reverse the two teams in a given division, and still have the same division into two teams. So, in this way the answer becomes .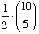
11. How many rearrangements of the letters of the word MINNEHAHA are there?
    Solution: There are 9 letters altogether. Proceed in stages, as follows:
    • There 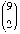 ways to choose 2 places for the N's.
    • After choosing places for the N's, there are 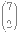 ways to choose 2 places for the H's.
    • After choosing places for the N's and the H's, there are 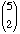 ways to choose 2 places for the A's.
    • Finally, there will be 3! = 6 ways to choose places for the remaining 3 letters.
    • Altogether the number of rearrangements is 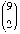··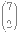 ·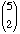3! = 36·21·10·6 = 45360.
12. ...
1. In how many ways can 12 crayons of distinct colors be distributed equally to 3 children?

Solution:··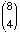= 495·70·1 = 34650.
 
2. In how many ways can 12 crayons be divided into 3 sets of 4 each? ?

Solution: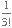··· 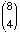= 34650/6 = 5775
13. = Exercise 2.4.16 in the notes.

Solution: Distributing the 10 quarters to 5 people amounts to solving the equation
      x₁ + x₂ + x₃ + x₄ + x₅ = 10,
where the solutions are to be integers > 0. By exercise 2.4.14, the number of solutions is thus:
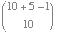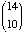=  = =1001
 
14. = Exercise 2.4.17 in the notes

Solution: The given equation is x + y + z=13, with x> 1, y> 0, and z> 6. We "invent" new unknowns,
setting a = x -1, b = y,and c = z -6. Then we have to solve a + b + c =6, with a, b,and call > 0.
So, we can apply the result of exercise 2.4.14 again, this time with n= 3 and k= 6.
 

Back to the class homepage.

For questions: roberts@math.umn.edu