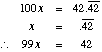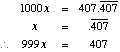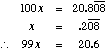Math 3113, Section 4

Math 3113, Section 4
Fall 1999
Solutions to chapter 5 and 6 review questions
(Problems 9 through 17)

- Convert each fraction to a terminating or repeating decimal:
- 9/ 22
solution: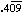
- 21/ 2048
solution: .01025390625
- 13/ 28
solution: 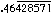
- Convert each repeating decimal to a quotient of integers and reduce to lowest terms. (Recall that 999 = 111·9 = 27·37.)
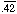
solution: 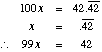
Hence: 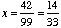
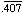
solution: 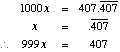
Hence: 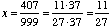
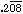
solution: 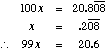
Hence: 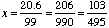
- Make a list of the distinct congruence classes modulo 9, in which each class is listed exactly once.
solution: According to the standard representation, thee congruence classes are:
[0]9, [1]9, [2]9, [3]9, [4]9, [5]9, [6]9, [7]9, [8]9,.
We can also name them as follows:
[1]9, [2]9, [3]9, [4]9, [5]9, [6]9, [7]9, [8]9, [9]9 .
- Find the standard representation for each of the following congruence classes:
- [71]12.
solution: 71 = 5·12 + 11, so that [71]12 = [11]12 .
- [81]9
solution: 81 = 9·9, so that [81]9 = [0]9 .
- [- 5]13
solution: [ - 5]13 = [ - 5 + 13]13 = [8]13.
- [- 13] 513
solution: [ - 13]5 = [ - 13 + 3·5]5 = [2]5.
- Find the standard class representative for each calculation:
- 11 + 9 mod 12
solution: 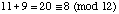 or [11 + 9]12 = [20]12 = [8]12 .
or [11 + 9]12 = [20]12 = [8]12 .
- 11 · 9 mod 12
solution: 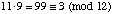 or [11 · 9]12 = [99]12 = [3]12 .
or [11 · 9]12 = [99]12 = [3]12 .
- 9 · 4 mod 12
solution: 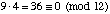 or [9 · 4]12 = [36]12 = [0]12 .
or [9 · 4]12 = [36]12 = [0]12 .
- 4 - 7 mod 8
solution: 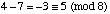 or [4 - 7]8 = [-3]8 = [5]8 .
or [4 - 7]8 = [-3]8 = [5]8 .
- This year, Christmas will be on a Saturday - day 7 of the week, if we start the numbering with Sunday as day 1.
On what day of the week will Christmas be next year? In the year 2001? Show appropriate mod 7 calculations to support your answer.
Suggestion: The fact that 2000 is a leap year while 2001 is not should be taken into account.
solution: 366 = 52·7 + 2, so that 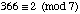
Therefore 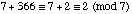 . So, Christmas will be on a Monday next year.
. So, Christmas will be on a Monday next year.
To proceed to the year 2001, note that 365 = 52·7 + 1, so that 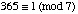 .
.
So, 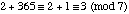 , and Christmas will be on a Tuesday in 2001.
, and Christmas will be on a Tuesday in 2001.
- Which of the following congruence classes have multiplicative inverses? Find the inverses of those that have inverses, and explain why the others don't have inverses.
- [5]8
solution: [5]8 · [5]8 = [ 25]8 = [1]8. Thus, [5]8 is its own inverse.
- [5]10
solution: [5]10 does not have an inverse, since 5 and 10 have a nontrivial GCD.
- [4]7
solution: [4]7 · [2]7 = [8]7 = [1]7. Thus, [2]7 is the inverse of [4]7.
- [4] 10
solution: [4]10 does not have an inverse, since 4 and 10 have a nontrivial GCD.
- Refer to the calculations from problem 3 to do the following:
- Write GCD(16,37) as 16a+ 37b
solution: We rearrange the two equations to obtain:
5 = 37 - 2·16
1 = 16 - 3·5
Now, we substitute form the first equation for the red 5 in the second equation:
1 = 16 - 3·(37 - 2·16)
1 = 16 - 3·37 + 6·16
So, finally:
1 = 7·16 - 3·37
- Write GCD(28,109) as 28a+ 109b
solution: We rearrange the three equations to obtain:
25 = 109 - 3·28
3 = 28 - 25
1 = 25 - 8·3 + 1.
Now we substitute from the second equation for the red 3 in the third equation:
1 = 25 - 8·(28 - 25)
1 = 9·25 - 8·28
Next, we substitute from the very first equation for the red 25 in our last equation:
1 = 9(109 - 3·28) - 8·28
1 = 9·109 - 27·28 - 8·28
1 = 9·109 - 35·28
- Use the answer from problem 16 to find multiplicative inverses of:
- [16]37
solution: The equation from 16a) gives:
[1]37 = [7]37·[16]37 - [3]37·[37]37 .
Since [37]37 = [0]37 , we conclude that [1]37 = [7]37·[16]37 .
Thus, [7]37 is the multiplicative inverse of[16]37 .
- [28]109
solution: The equation from 16b) gives:
[1]109 = [9]109·[109]109 - [35]109·[28]109 .
Since [109]109 = [0]109 , we conclude that [1]109 = [ - 35]109·[28]109 .
Thus, [ - 35]109 is the multiplicative inverse of[28]109 .
We also can write the answer as [ - 35 + 109]109 = [74]109

Back to the
review questions.
For questions: roberts@math.umn.edu