Math 3113, section 4

Fall 1999

Solutions to the second test

  1. (28 points) This problem is about license plates consisting of 3 letters followed by 3 numbers,

    2. for instance ABC 123.
    1. Find the number of license plates which have a triple letter.
      (So, AAA 012 would be a particular instance.)
       
      Solution: 26·1·1·10·10·10 = 26,000
       
    2. Find the number of license plates which have a triple number.
      (So, XYZ 999 would be a particular instance.)
       
      Solution: 26·26·26·10·1·1 = 175,760
       
    3. Find the number of license plates which have a triple letter anda triple number.

      4.  
      Solution: 26·1·1·10·1·1 = 260
       
    4. Find the number of license plates which have a triple letter ora triple number.
       
      Solution: 26,000 + 175,760 - 260 = 201,500
       
  2. (14 points) Expand by using the binomial theorem:
     
    Solution: (x - 2y)5 = 20x5y0 - 5·2x4y1 + 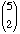 · 22x3y2 - 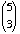 · 23x2y3 + 5·24x1y4 - 25x0y5,

    so that (x - 2y)5 = x5 - 10x4y + 40x3y2 - 80x2y3 + 80xy4 - 32y5.
     

  3. (16 points) A certain club has 20 members.
    1. In how many ways is it possible to nominate 4 members for the offices of President, Vice President, Secretary, and Treasurer (in that order ... ) ?
       
      Solution: 20·19·18·17 = 116,280
       
    2. In how many ways is it possible to select a committee consisting of 4 members of the club?
       
      Solution: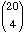 =  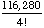= 4845
       
  4. (14 points)
    Two pairin a five card poker hand has two of one kind, two of another kind, and the fifth card of a third kind, for instance 2-2-Q-Q-A. Determine the number of two pair hands.
     
    Suggestion: Check to be sure that your answer doesn't count anything more than once!
     
    Method 1: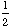· {·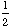· 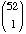3 ·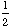··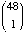 3}· 44 = 2808 · 44 = 123,552
     
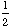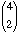    Method 2:· {13 ·· 12 ·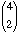 }· 44 = 2808 · 44 = 123,552
     
    Remark: the "extra" factor of 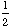 outside the brackets is to eliminate duplicates because the two pairs in a given hand could have been chosen in two different orders. For instance, we should not count 2-2-Q-Q-A and also Q-Q-2-2-A as being different hands!
     
    Another way to see this. If we just do this calculation:
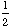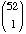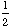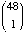          { ·· 3} ·{ · · 3} · 44 ,
    then we are counting the ways to do the following steps: So, if we have chosen two given pairs in a particular order, we can get the same hand by choosing the same two pairs in the the opposite order. To eliminate the duplication, we have to multiply by 1/2.
     
  5. (14 points) How many rearrangements of the letters of the word ALABAMA are there?
     
    Solution: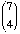· 3! = 210
    (We first choose places for the four A's, and then distribute the other 3 letters among the remaining places.)
     
  6. (14 points) In how many ways can 10 identical coins be distributed to 3 people?
     
    Suggestion: This can be considered as counting solutions of x1 + x2 + ... + xn = k.
    In that case, one has to determine the correct values for nand k.
     
    Solution: We take n= 3 and k= 10. So, the number of solutions is ,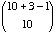
    or 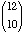 =  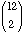= 66.
     

For questions: roberts@math.umn.edu

Back to class homepage.