NOTE: It is also strongly recommended to review past homework problems and your notes from group work in class. The problems on this page do not represent every type of question that could occur on the test. Note also that this problem list is considerably longer than the test will be.

Click here to see the solutions to problems 1 through 8.
Click here to see the solutions to problems 9 through 17.

1. Find prime factorizations of the following numbers:
1. 28
2. 68
3. 323
4. 108
5. 109
    
2. Using the prime factorizations from the previous problem, find the following greatest common divisors and least common multiples:
1. GCD(28,68) and LCM(28,68)
2. GCD(28,108) and LCM(28,108)
3. GCD(28,323)
4. GCD(68,323)
5. GCD(28,109)
    
3. Use the Euclidean algorithm to find the following GCD's:
1. GCD(16,37)
2. GCD(28,109)
3. GCD(1003,1999)
    
4. In each case, find the next five numbers in the given base:
1. 11011_two
2. 2221_three
3. 2AD _sixteen
    
5. Convert to bases 2, 3, and 16:
1. 79
2. 257
    
6. Convert to base 10:
1. 100011_two
2. 177_nine
3. BBB _twelve
    
7. Do the indicated conversions:
1. 110111011_two to base eight
2. 21201_three to base nine
    
8. Do the following calculations in the indicated bases. Show your work, including which numbers were carried. Check your answer by converting to base 10 and doing appropriate base 10 calculations:
1. Add in base eight: 6142_eight and 2457_eight
2. Subtract in base eight: 651_eight from 6142_eight
3. Multiply in base five: 423_five by 214 _five
    
9. Convert each fraction to a terminating or repeating decimal:
1. 9/22
2. 21/2048
3. 13/28
    
10. Convert each repeating decimal to a quotient of integers and reduce to lowest terms. (Recall that 999 = 111·9 = 27·37.)
1. 
2. 
3. 

 
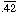
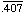
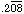
11. Make a list of the distinct congruence classes modulo 9, in which each class is listed exactly once.
     
12. Find the standard representation for each of the following congruence classes:
1. [71]₁₂
2. [81]₉
3. [- 5]₁₃
4. [- 13] ₅
    
13. Find the standard class representation for each calculation:
1. 11 + 9 mod 12
2. 11 · 9 mod 12
3. 9 · 4 mod 12
4. 4 - 7 mod 8
    
14. This year, Christmas will be on a Saturday - day 7 of the week, if we start the numbering with Sunday as day 1. On what day of the week will Christmas be next year? In the year 2001? Show appropriate mod 7 calculations to support your answer.
    Suggestion: The fact that 2000 is a leap year while 2001 is not must be taken into account.
     
15. Which of the following congruence classes have multiplicative inverses? Find the inverses of those that have inverses, and explain why the others don't have inverses.
1. [5]₈
2. [5]₁₀
3. [4]₇
4. [4] ₁₀
    
16. Refer to the calculations from problem 3 to do the following:
1. Write GCD(16,37) as 16a+ 37b
2. Write GCD(28,109) as 28a+ 109b
    
17. Use the answer from problem 16 to find multiplicative inverses of:
1. [16]₃₇
2. [28]₁₀₉

Back to the class homepage.