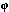 : U - > X, where U is a subset
of A1 whose complement
(in A1) is finite,
and the mapping has the following
properties:
: U - > X, where U is a subset
of A1 whose complement
(in A1) is finite,
and the mapping has the following
properties:Copyright (©) 1997 by Joel Roberts.
Let's begin by saying what we mean by a rational parametrization
of a plane curve. Thus, let X be an irreducible algebraic curve
in A2.
A rational parametrization
of X is a map 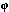 : U - > X, where U is a subset
of A1 whose complement
(in A1) is finite,
and the mapping has the following
properties:
: U - > X, where U is a subset
of A1 whose complement
(in A1) is finite,
and the mapping has the following
properties:
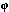 (t )
are rational functions of t ;
(t )
are rational functions of t ;
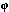 is a
finite set.
is a
finite set. OUR FIRST EXAMPLE comes from the text. Thus, let X be a plane curve of degree 3 with a node at the origin. Central projection from the origin maps X - {(0,0)} to the line x = 1 in an essentially bijective fashion, and the inverse of the projection provides the desired rational parametrization. Explicitly, we take X to be given by the following equation:
 : X - {(0,0)} ->
A1
given by the following formula:
: X - {(0,0)} ->
A1
given by the following formula:  ((x,y)) = (1,t) ,
((x,y)) = (1,t) ,
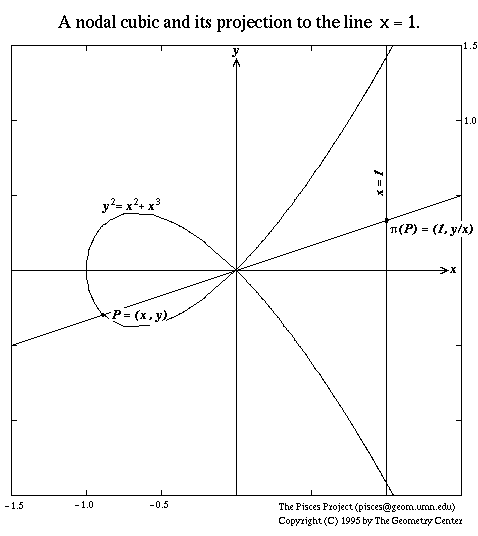
To find the parametrization, we set t = y/x, so that y = tx. We substitute this into the defining equation of our curve, and then solve for x in terms of tto the extent that this is possible. Thus:
 (t) = (t - 1,
t (t - 1))
= (t - 1, t 2
- t )
(t) = (t - 1,
t (t - 1))
= (t - 1, t 2
- t )OUR SECOND EXAMPLE is the curve which is given in polar coordinates by the following equation:
 ).
).  )
= 4cos3
)
= 4cos3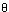 - 3cos
- 3cos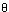 .
.
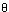 - 3r 3cos
- 3r 3cos
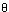
As in the previous example, we identify A1 with the line x = 1, and then construct the projection from the origin exactly as in the previous example. This is shown in the following figure:
To obtain a parametrization, we proceed as in the first example. Thus, we substitute y = tx into the defining equation of our curve and then solve for x in terms of t, as follows:
SOME COMMENTS The parametrization
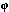 (t ) is undefined for
t = i and for t = -i. This fact, of course,
is invisible when we are looking at the set of real points. The values
t =
(t ) is undefined for
t = i and for t = -i. This fact, of course,
is invisible when we are looking at the set of real points. The values
t = 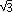 and
t = -
and
t = - 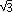 are both mapped to (0,0).
It also is intuitively valid, at least when K = C, to claim
that t =
are both mapped to (0,0).
It also is intuitively valid, at least when K = C, to claim
that t =  is mapped to (0,0), because
is mapped to (0,0), because
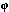 (t ) gets close
to (0,0) when |t | becomes very large.
(t ) gets close
to (0,0) when |t | becomes very large.
BOTH OF THESE EXAMPLES are instances of a more general result. In order to state this result, we need some terminology. So, let K be an algebraically closed field. If f (x,y) is an irreducible element of the polynomial ring K[x,y], then we say that the curve X = V(f ) is an irreducible plane curve. More generally, a hypersurface in An whose defining polynomial is irreducible is called an irreducible hypersurface. By definition, the degree of an irreducible plane curve, or more generally an irreducible hypersurface, is the degree of its defining polynomial.
If X = V(f ) is a plane curve, we will say that X has a point of multiplicity = m at (0,0) if (0,0) is a point of X and
PROPOSITION. Let X be an irreducible plane curve of degree d . If X has a point of multiplicity d - 1, then X has a rational parametrization.
PROOF. The hypothesis implies that the defining defining equation of X is of the following form:
Q.E.D.
The parametrization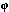 is
undefined at values of t where
Fd (1,t) = 0,
while the values of t such that
Fd - 1(1,t)= 0
are mapped to the origin. Since our field is algebraically closed,
both of these things will definitely occur, unless either
Fd - 1(1,t)
or Fd (1,t)
is a nonzero constant. (That situation happens when
Fd - 1
or Fd respectively
is a power of x.
is
undefined at values of t where
Fd (1,t) = 0,
while the values of t such that
Fd - 1(1,t)= 0
are mapped to the origin. Since our field is algebraically closed,
both of these things will definitely occur, unless either
Fd - 1(1,t)
or Fd (1,t)
is a nonzero constant. (That situation happens when
Fd - 1
or Fd respectively
is a power of x.
More generally, let X be an irreducible curve of degree d with a point of multiplicity m at (0,0). Then the irreducible defining polynomial of X is of the following form:
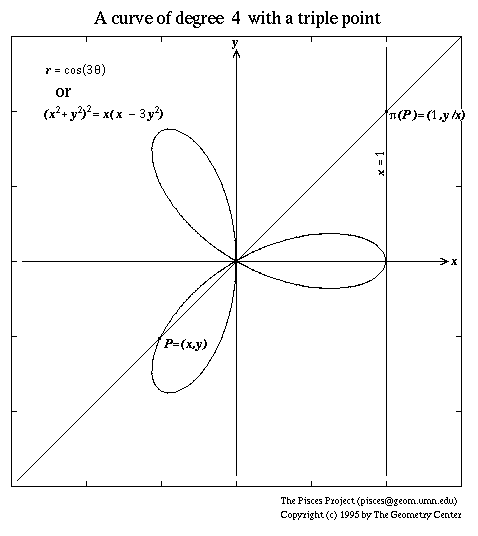
Since K is algebraically closed, the homogeneous polynomials Fm (x,y) and Fd (x,y) factor as products of homogeneous linear polynomials. Indeed, the linear factors (except, possibly, for powers of x) correspond bijectively to the roots of Fm (1,t) and Fd (1,t) respectively. BY DEFINITION, the zero set of Fm (1,t) is called the tangent cone of X at the origin. Since Fm (1,t) is a product of homogeneous linear polynomials, it follows that the tangent cone is a union of lines through the origin. For instance, in the case of our fourth degree curve with a triple point the initial form factors as follows:
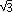 y)(x -
y)(x -
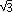 y) .
y) .
AN ILLUSTRATION showing this curve and its tangent cone at the origin is linked here.
THE FACTORS OF THE
HIGHESTDEGREE
FORM were seen to correspond to asymptotic
directions at infinity when K = C. In
general, we can understand this in another way by "homogenizing"
the equation f(x,y) = 0 to obtain the equation
F(X,Y,Z) = 0 of the projective closure
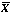 , specifically:
, specifically:
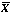 with the line at infinity,
i.e. the line Z = 0. We conclude that this
intersection is the solution set of the equations:
with the line at infinity,
i.e. the line Z = 0. We conclude that this
intersection is the solution set of the equations:
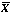 intersects the line at infinity correspond bijectively to the
distinct linear factors of the highest degree form of the highest
degree form Fd (X,Y) .
(In the present context, we understand two linear factors to be
distinct if neither one is a constant multiple of the other.)
intersects the line at infinity correspond bijectively to the
distinct linear factors of the highest degree form of the highest
degree form Fd (X,Y) .
(In the present context, we understand two linear factors to be
distinct if neither one is a constant multiple of the other.)
AS A FINAL EXAMPLE to illustrate both of these concepts, we consider the plane curve of degree 5 whose equation is:
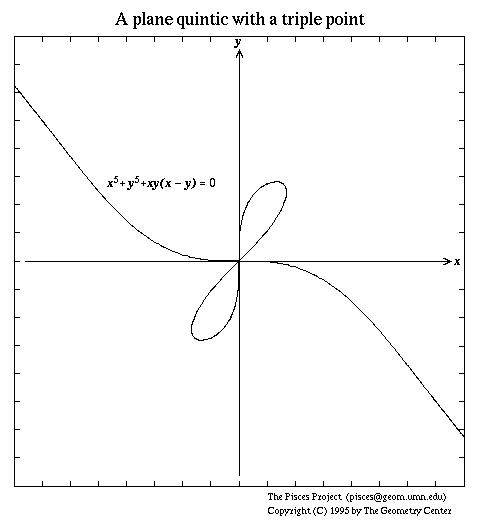
RELATED EXERCISES ARE LINKED BELOW.
Last updated October 10, 1997.
Please send comments and/or corrections to:
Joel Roberts
351 Vincent Hall
625-1076
e-mail:
roberts@math.umn.edu
http://www.math.umn.edu/~roberts