The picture on the left shows a graph of
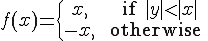
The red line shows the cross section x=0, while the green line highlights the cross section y=0. Click and drag on the picture to rotate it; type "F" after clicking on the picture to view the cross sections without the surrounding surface.1
For this function,
- fy(0,0)=0; it's the slope of the line tangent to the red curve at the point of intersection.
- fx(0,0)=1; when y=0, we have f(x,y)=f(x,0)=x, and the derivative of this function with respect to x is 1, whether we're at the origin or anywhere else along the line.
Both of the partials exist at the origin, but the function clearly is not differentiable at (0,0); if the surface had a tangent plane there it would simultaneously have to be both z=x and z=-x.
Most calculus books include a theorem saying that if the partials are continuous at and around a point, a function is differentiable. The reason this example doesn't contradict the theorem is that the partials are not continuous at the origin.
However, it's also possible that a function is differentiable with discontinuous partials.
1 Why F? The applet on this page uses F to toggle the display of polygon Faces, which are the computer graphics objects which make up the displayed surface.