This animation shows that f(x) is not differentiable at the origin. It shows the secant line through (0,f(0)) and (h,f(h)). If f(x) were differentiable, these secant lines should approach a tangent line as h approaches zero. You can see in this animation that this doesn't happen; the secant line continues to osciallate between y=x and y=-x.
What happens when you replace x with x2?
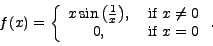
This function is continuous at the origin; many books prove this as an application of the Squeeze Theorem. Because
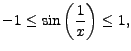 ,
it follows that
,
it follows that
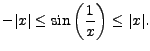 .
The Squeeze Theorem says
.
The Squeeze Theorem says
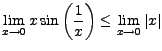 |
||
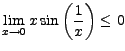 |
Hence
![]() , so
, so ![]() is continuous at
is continuous at ![]() .
.
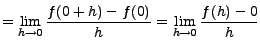 |
||
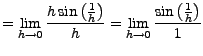 |
||
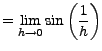 |