This animation shows that g(x) is differentiable at the origin. It shows the secant line through (0,g(0)) and (h,g(h)). The secant lines quickly approach the tangent line y=0 as h approaches 0.
What happens when you replace x2 with x?
Like its relative
![]() ,
, ![]() is continuous at the origin; as with
is continuous at the origin; as with ![]() , you can prove this with the Squeeze Theorem. Unlike
, you can prove this with the Squeeze Theorem. Unlike ![]() , however,
, however, ![]() is also differentiable at the origin! The extra power of
is also differentiable at the origin! The extra power of ![]() is just enough to make the limit exist:
is just enough to make the limit exist:
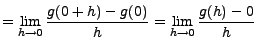 |
||
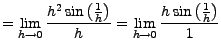 |
||
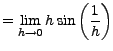 |
||
That last limit is evaluated with the Squeeze Theorem; it's actually exactly the same limit you need to evaluate to show that ![]() is continuous.
is continuous.
You can see visual evidence in the applet on the left that the derivative exists at the origin. Move your mouse over the picture to the left to start the animation; you may also have to click on the picture before it starts.