Elliptic Paraboloid
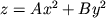
(where A and B have the same sign)
|
Display Gridlines: |
This is probably the simplest of all the quadric surfaces, and it's often the first one shown in class. It has a distinctive "nose-cone" appearance. This surface is called an elliptic paraboloid because the vertical cross sections are all parabolas, while the horizontal cross sections are ellipses. Occasionally we get sloppy and just refer to it simply as a paraboloid; that wouldn't be a problem, except that it leads to confusion with the hyperbolic paraboloid. The cross sections on the left are for the simplest possible elliptic paraboloid: One important feature of the vertical cross sections is that the parabolas all open in the same direction. That isn't true for hyperbolic paraboloids! Note that in this case, the horizontal cross sections are actually circles, but this isn't always the case. In fact, whenever A and B are not equal, the paraboloid will be wider in one direction than the other. You can use the second picture to investigate how these coefficients affect the shape of the surface. It shows the paraboloid z = A x2 + B y2 over the square domain -1 ≤ y ≤ 1. If you change the domain to a disk, you will see the portion of the paraboloid for which 0 ≤ z ≤ 8. When you change A and B, the domain will change accordingly. Here are a few things to think about:
|





