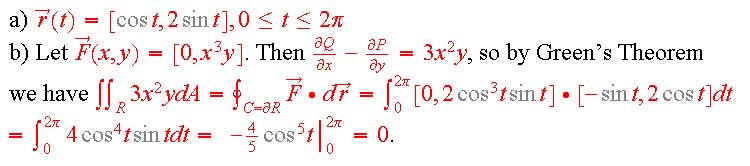

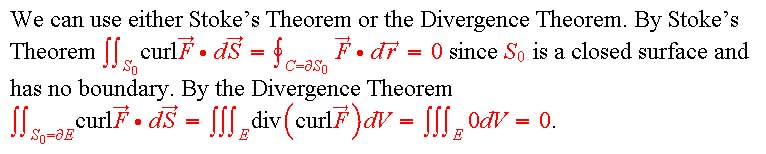

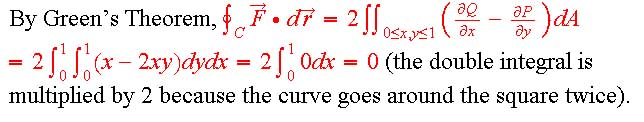

a) A curve that is part of the boundary of a region in the plane has positive orientation if when you walk around the curve in the direction of the orientation the region is on your left.
b) The outer circle should have counterclockwise orientation; the inner two circles should have clockwise orientation.
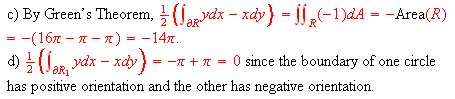
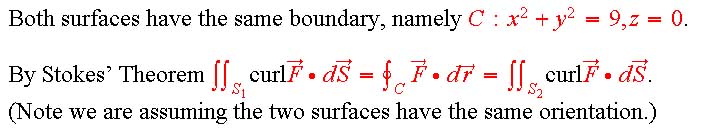
b)
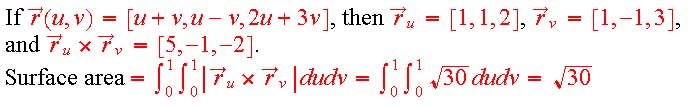
Closed: (a), (c) (remember, "closed" is stronger than "not open")
Connected: (a), (c), (f)
Simply Connected: (a), (f)


Yes, F is conservative; f would be the integral of P with respect to x plus the integral of Q with respect to y.
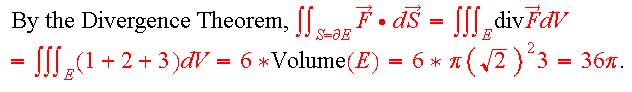
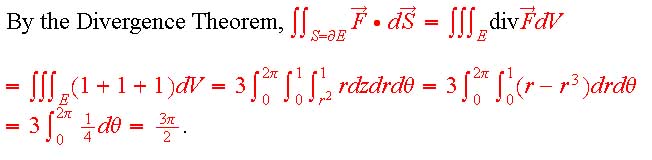

Use Green's Theorem separately for each region; in each one you'll integrate the function 8, so you get 8 times the area of the regions:
This is a repeat of #2; sorry!
I1 = e-a - e-c > 0
I2 = (b-d) e-a-c ( ea + e-c) / (a-c) < 0
I2 = Sqrt( (a-c)2 + (b-d)2 ) ( ea - ec) / (a-c) > 0
You can explain the signs of I1 and I2 by considering the direction of motion and the direction of the vector fields you're integrating -- < e-x, 0 > and < 0, e-x > , respectively. The third must be positive because it's a line integral of a scalar function, and the function is always positive.