What do students do after the REU? Previous students have subsequently gone on to graduate school at Brown (2), CalTech, Columbia, Cornell (2), Georgia Tech, Harvard, Maryland, McGill, Moscow, NYU (2), Oxford, Princeton, Purdue U, U Chicago (2), UC Boulder, UC Irvine, UIUC, UMass, U Mich, Northwestern, U Minnesota (3), 7 received NSF Graduate Fellowships.
What happens in projects - two examples:
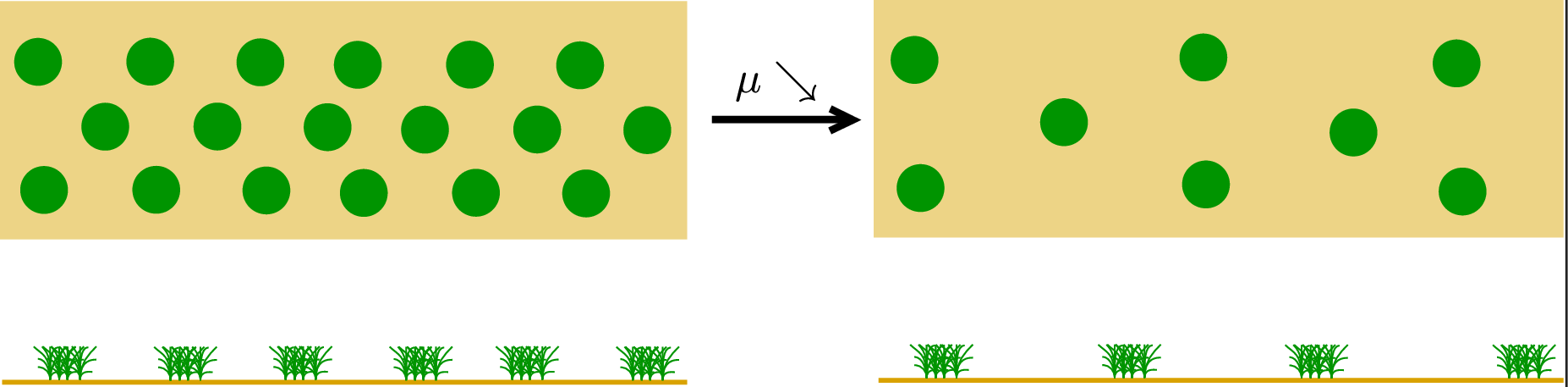
Self-organized sacrifice, or, the disappearance of vegetation patches
Vegetation in arid and semi-arid climates is organized in patches, benefiting from synergistic effects of higher density in the patches and saving overall water resources. We studied the effect of decreasing overall rainfall on such self-organized vegetation patterns in an idealized pattern-forming model. As a parameter, representing average rainfalls, decreases, a pattern slowly adapts until a moment of crisis when one or several patches disappear. We predict these moments of crisis and how many patches disappear in such a crisis. The results are somewhat universal across models. Mathematically, we study reduced ordinary differential equations with a slow parameter and a trivial equilibrium that undergoes subsequent pitchfork bifurcations as the parameter evolves. Intriguingly, the predictions are based on spatio-temporal resonances, commonly associated with instability in dispersive waves and plasma dynamics.
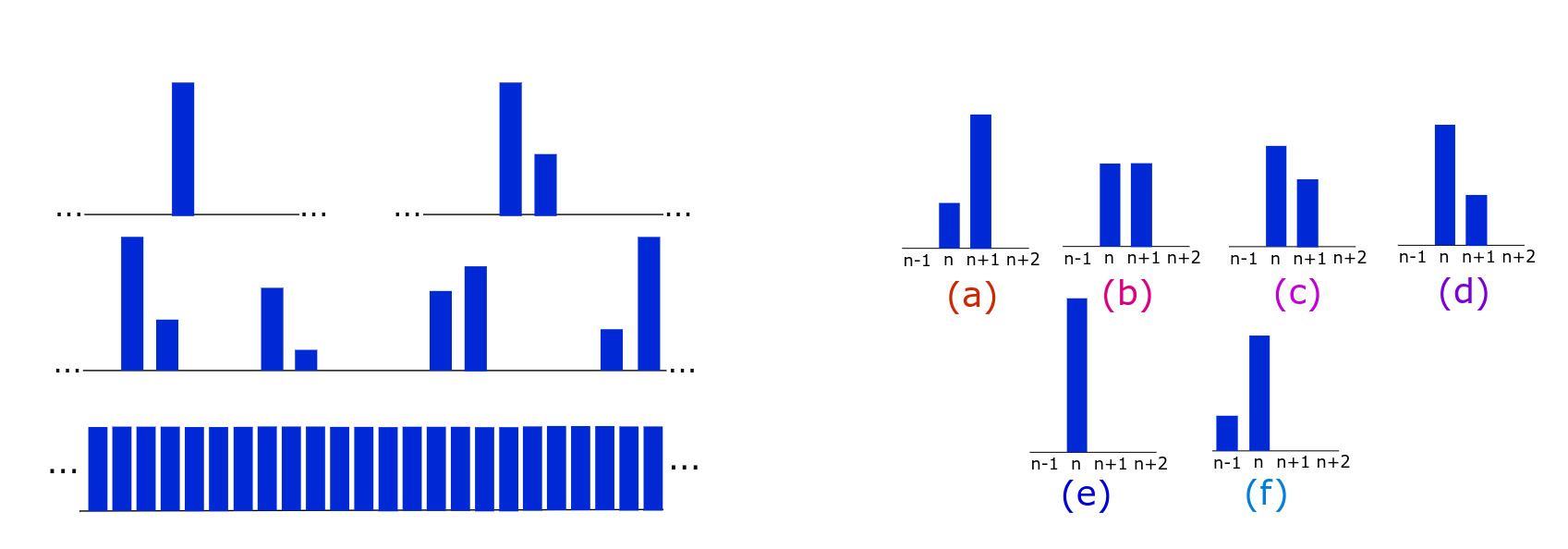
Bias and bounded confidence, or, the shifting of opinion in groups
How do people change their opinions? This simple question has led to decades of mathematical study, and one foremost class of models, called bounded confidence models, posit the following: people will talk, and compromise, but they will only compromise with those whose opinions are close to theirs. We study the addition of bias to one such model on a lattice. In particular, we look at how bias causes clusters of opinions to move. We find that with a certain form of bias called self-incitement, where people in larger same-opinion groups are more likely to shift their opinion, a cluster will move but retain its shape. We prove existence of such moving clusters for bias close to a critical value, and use numerical continuation to explore the whole parameter space. The proof in the subcritical regime relies on nonlocal center manifold expansions for the functional equation in a traveling frame. In the small bias regime, we also use ideas from geometric singular perturbation theory to get expansions for cluster speed. Notably, for other bias terms which do not display self-incitement, one does not see this movement - clusters either disperse or fail to propagate.
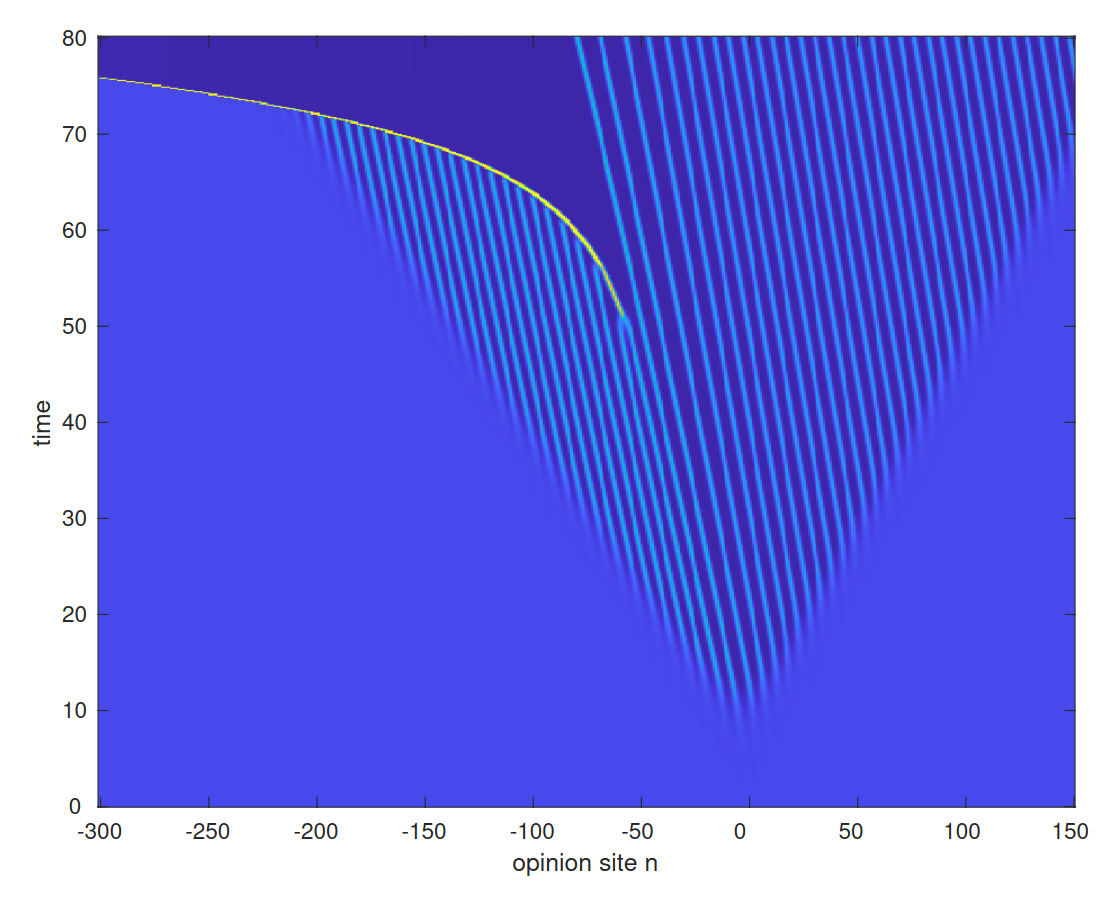
-
- A. Asch, M. Avery, A. Cortez, A. Scheel
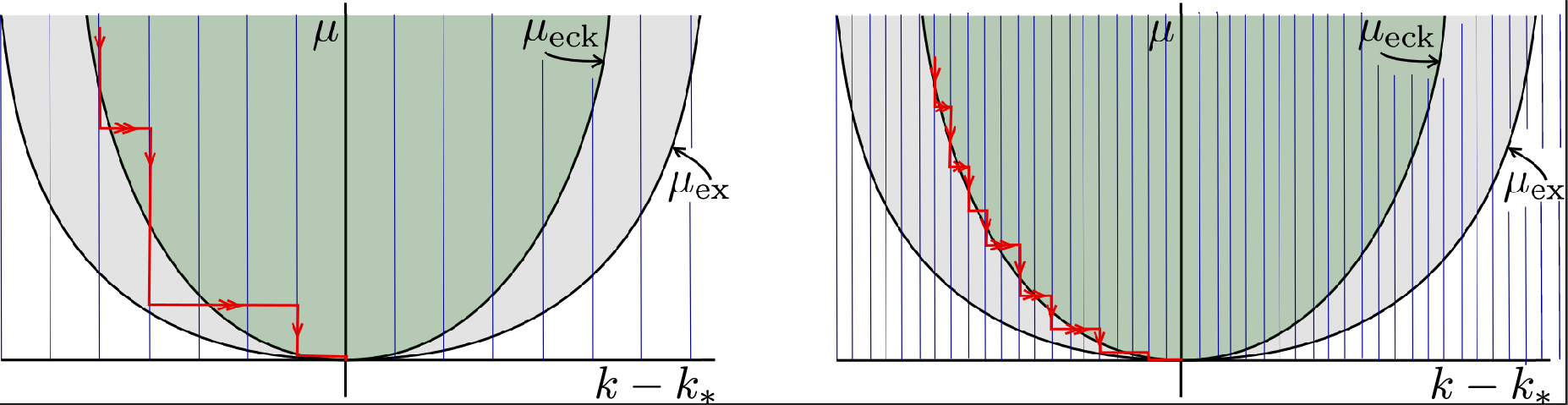
Slow passage through the Busse balloon -- predicting steps on the Eckhaus staircase. (PDF)
-
- O. Cannon, T. Bondurant, M. Whyte, A. Scheel
Shifting consensus in a biased compromise model (PDF)
SIAM J. Appl. Dyn. Sys., to appear -
- K. Chen, Z. Deiman, R. Goh, S. Jankovic, A. Scheel
Strain and defects in oblique stripe growth (PDF)
Multiscale Model. Simul. 19 (2021), 1236-1260 -
- M. Avery, C. Dedina, A. Smith, A. Scheel
Instability in large bounded domains — branched versus unbranched resonances (PDF)
Nonlinearity 34 (2021), 7916-7937 - M. Avery, R. Goh, O. Goodloe, A. Milewski, A. Scheel
Growing stripes, with and without wrinkles (PDF) [Moduli space movie with delicate arch, Supplementary materials]
SIAM J. Appl. Dyn. Sys. 18 (2019), 1078-1117-
- N. Ankney, M. Avery, T. Khain, A. Scheel
Pinning and Depinning: from periodic to chaotic and random media (PDF)
Chaos 29, 013127 (2019) - R. Samuelson, Z. Singer, J. Weinburd, A. Scheel
Advection and autocatalysis as organizing principles for banded vegetation patterns (PDF)
J. Nonlinear Science 29 (2019), 255-285- P. Flynn, Q. Neville, A. Scheel
Self-organized clusters in run-and-tumble processes (PDF)
DCDS-S 13 (2020), 1187-1208- R. Goh, R. Beekie, D. Matthias, J. Nunley, A.Scheel
Universal wavenumber selection laws in apical growth (PDF)
Phys. Rev. E 94 (2016), 022219.-
- T. Anderson, G. Faye, A. Scheel, D. Stauffer
Pinning and unpinning in nonlocal systems (PDF)
J. Dyn. Diff. Eqns.28 (2016), 897-923.. -
- C. Browne, A. Dickerson. Mentors: G. Faye, A. Scheel.
Coherent structures in scalar feed-forward chains (PDF)
SIURO 7 (2014), 306-329. -
- K. Bose, T. Cox, S. Silvestri, P. Varin. Mentors: M. Holzer, A. Scheel.
Invasion fronts and pattern formation in a model of chemotaxis in one and two dimensions. (PDF)
SIURO 6 (2013), 228-245. -
- M. Kotzagiannidis, J. Peterson, J. Redford, A. Scheel, Q. Wu
Stable pattern selection through invasion fronts in closed two-species reaction-diffusion systems. (PDF)
In RIMS Kokyuroku Bessatsu B31 (2012), Far-From-Equilibrium Dynamics, eds. T. Ogawa, K. Ueda , pp 79-93. -
- R. Goh, S. Mesuro, A. Scheel
Spatial wavenumber selection in recurrent precipitation (PDF)
SIAM J. Appl. Dyn. Sys. 10 (2011), 360-402. - R. Goh, S. Mesuro, A. Scheel
Coherent structures in reaction-diffusion models for precipitation (PDF)
Special volume on "Precipitation patterns in reaction-diffusion systems", Research Signpost (2010), 73-93.