Chapter 7 solutions
Exercise 7.1.11
The total number of bridge hands isExercise 7.3.1, part (i)
Two cards are drawn at random from a standard deck. The events are "both cards aces" [ which we'll call E] and "both cards kings" [ which we'll call F].
Last update: May 4, 2001 at 11:00 a.m.
To get the latest version, click the "reload"
or "refresh" button on your browser window.
Solutions to the following exercises are presented here:
Chapter 7 solutions Exercise 7.1.11 Exercise 7.3.1, part (i)
![]() = 635,013,559,600.
There are just 4 perfect hands, so that p =
= 635,013,559,600.
There are just 4 perfect hands, so that p = ![]() = 0.0000000000063
= 0.0000000000063
On the one hand, E![]() F -- the simultaneous occurrence of both E and F -- would be a situation where both cards were aces and also kings. This is clearly impossible. Therefore
p(E
F -- the simultaneous occurrence of both E and F -- would be a situation where both cards were aces and also kings. This is clearly impossible. Therefore
p(E![]() F) = 0.
F) = 0.
On the other hand, we can calculate both p(E) and p(F) by reasonably familiar methods. The number of ways to choose 2 cards from a deck of 52 cards is ![]() Since there are 4 aces, the number of ways to choose 4 aces is
Since there are 4 aces, the number of ways to choose 4 aces is ![]() Thus p(E) =
Thus p(E) = ![]() = .004525. By an identical calculation, we find that p(F) = .004525. Therefore it follows that p(E)·p(F) = .004525·.004525 = .0000205.
= .004525. By an identical calculation, we find that p(F) = .004525. Therefore it follows that p(E)·p(F) = .004525·.004525 = .0000205.
Comparing the two answers, we see that p(E
![]() F)
F)
![]() p(E)·p(F). This shows that the two events are dependent, i.e. not independent.
p(E)·p(F). This shows that the two events are dependent, i.e. not independent.
Some comments:
(1) The two events happen to be disjoint, since they can't happen together. So, we see that disjointness is a special type of being dependent (but not the other way around!!).
(2) The method used here is the only correct way to do this sort of problem. In other words the values of p(E![]() F) and p(E)·p(F) must be calculated separately. We check whether the two answers are equal or unequal in order to finally solve the problem.
F) and p(E)·p(F) must be calculated separately. We check whether the two answers are equal or unequal in order to finally solve the problem.
Exercise 7.3.1, part (iv
) This time, just one card is drawn from the deck. One of the events is "the card is a spade" [ we'll call this E], and the other event is "the card is an ace" [ we'll call this F].Exercise 7.5.7
Of the 25 students, 10 have blue eyes and 12 are female.Exercise 7.5.8
The requirement of sampling without replacement changes the problem considerably,Exercise 7.5.9 Of the 25 students, 6 are blue-eyed males a
nd 4 are brown-eyed females. So the probability that a randomly selected stud
ent is a blue-eyed male is .24. The probability that a randomly selected stud
ent is a brown-eyed female is .16. Miscellaneous problems from the
1/25/01 class handout Questions?
roberts@math.umn.edu
Back to the top of the page.
![]() = 26·51 = 1326.
= 26·51 = 1326.![]() = 6.
= 6.
13(52 - 13) =13·39 = 507.
The number of outcomes where both cards are spades is:
![]() = 13·6 = 78.
= 13·6 = 78.
So, altogether there are 507 + 78 = 585 outcomes where at least one card is a
spade.
Comments:
= .0045.
![]() = .44.
= .44.
![]() =.0023.
=.0023.
![]() = .0023. So,
= .0023. So, ![]() , and the two events are not independent.
, and the two events are not independent.
Back to the HW assignments.
Back to the class homepage.
Chapter 8 solutions
Exercise 8.1.6
Exercise 8.1.7
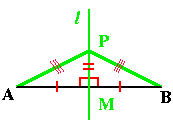
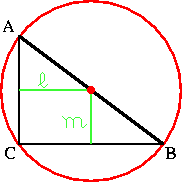
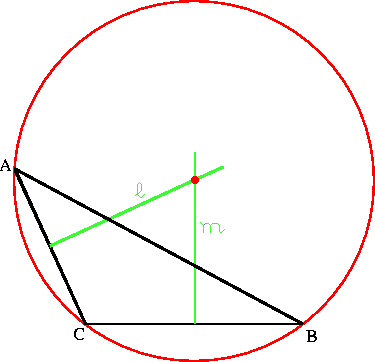
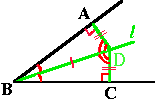
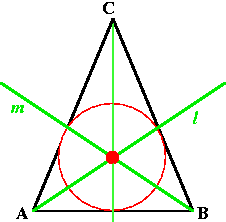
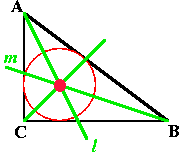
In each figure, l is the perpendicular bisector of AB, and m is the perpendicular bisector of BC. (These are shown in green.) The circumcenter is shown as a red dot at the intersection point of the two perpendicular bisectors, and the third one (not always shown) also will pass through that point.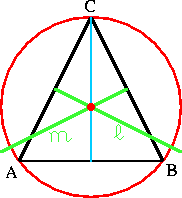
Exercises 8.1.10 and 8.1.11
Exercise 8.2.7
Exercise 8.2.8 Exercise 8.2.10 Exercise 8.2.14 Exercise 8.2.18 Exercise 8.2.20 Exercise 8.3.1 First part. In the first figure in "suggested setup", the point on the x-axis is (x,0). So, the length of the horizontal leg of the right triangle is x, and the length of the vertical leg is y. Therefore, according to Pythagoras, the length of the hypotenuse is (x2 + y2)1/2. But this is ||P||, by the definition of the norm. Second part. In the second figure in "suggested setup", we fill appropriate portions of the two dotted
lines to show a right triangle. The vertex at the right angle is joined
to (a,b) by a horizontal line. Therefore its
y-coordinate = b. (The same as the y-coordinate
of (a,b).) In the same way, this vertex is joined to (c,d)
by a vertical line, so that its x-coordinate = c.
Thus, the vertex at the right angle is (c,b).
So far, so good. Using what we just figured out, we see that the length of the horizontal leg of the right triangle is c-a, and the length of the vertical leg is d-b. Using the theorem of Pythagoras again, we see that the length of the hypotenuse is ((c-a)2 + ((d-b)2)1/2. In other words, this formula gives the distance from P to Q.
Aren't we finished yet?? Well, we were supposed to compare this distance with the norm of Q -P. So, we do the vector subtraction: By inspection, i.e. by just looking, we see that this is the same as our formula for the distance from P to Q.
Exercise 8.3.2 Second part: By doing the vector addition, we see that A + B = C. (If you don't see this right away, check it on a piece of scratch paper.) But our calculations clearly show that ||C|| is not equal to ||A|| + ||B||.
Indeed, 6.32 is a lot smaller than 13 + 9.22. Further note (optional): In physics, we might use the vectors A and B to represent forces acting on some object. In a picture, we would represent these forces by arrows. The respective norms represent the lengths of the arrows, or the magnitude of the forces. For instance, suppose that a truck is being driven across a bridge during a hurricane. The bridge is acted upon by the wind and by the weight of a truck on the bridge. The wind acts more or less horizontally, and the weight of the truck acts in a downward direction (if the truck isn't blown off the bridge, anyway). We get the total force acting on the bridge by doing vector addition.
Exercise 8.3.4 Method 1: Using the theorem. We work with the vector D = (-4,7). According to the theorem, the norm (or "length") of this vector represents the distance that Joe travels in 1 hour. The value of this is ||D|| = ((-4)2 + 72)1/2 = (16 + 49)1/2= 651/2 (or about 8.06 units of distance). So, the distance that he travels in three hours is 3·651/2, or about 24.19 units of distance. Method 2. We work with the given formula P(t) = (9,11) + t(-4,7). So, his position at time t = 0 is P(0) = (9,32). His position at time t = 3 is P(3) = (-3,32). So, the total "displacement" is found by vector subtraction: Thus, in 3 hours, the x-coordinate of his position changes by -12, and the y-coordinate of his position changes by 21. The distance that he travels is ((-12)2 + 212)1/2 = (144 + 441)1/2 = 5851/2, or about 24.19 units of distance. Chapter 11 solutions Exercise 11.1.13 Solution:
Exercise 11.5.2 The mean is The standard deviation is s = Exercise 11.5.3 The point here is just to calculate the z-values. Corresponding to x = 30.5, we have z = Using the same formula with x = 29.5, we get: z = Exercise 11.5.4 Corresponding to z = 0.1, Table 11.6 gives A(z) = 0.398. This gives the area under the normal curve between z = 0 and z = 0.1. By the symmetry of the normal curve, we have exactly the same amount of area between z = -0.1 and z = 0. Therefore, the total area between z = -0.1 and z = 0.1 is 0.398 + 0.398 = 0.796 Exercise 11.5.5 The probability of getting exactly k sevens in n rolls of the dice is: Therefore, we have to calculate the following number: We have: Therefore: The fact that these two answers agree so closely shows how
closely the independent trials process is approximated by the normal curve. Exercise 11.5.7 The mean is once again given by the formula Exercise 11.5.8 Since q = 1 - p = .1, we have s = Exercise 11.5.9 Looking at Figure 11.4 in the text, we need to make the total shaded area be 80% of the area under the normal curve. Exercise 11.5.10 We need to solve the equation .9n + .85 We can re-arrange this as follows: .85 To get rid of the square root, we square both sides: (.85 .065025n = 62500 - 450n + .81n2, or: .81n2 - 450.065025n + 62500 = 0. We use the quadratic formula to solve this: n = Therefore, the roots are n = 282.55, and n = 273.09. The smaller root gives has the corresponding mean: So, this choice satisfies the original equation The conclusion is that they can sell 273 seats.
Questions?
roberts@math.umn.edu
Back to the top of the page.
Back to the HW assignments. Back to the class homepage.
![]() = (8,6) - (8,6) = (0,0)
= (8,6) - (8,6) = (0,0)
=(5,-3) + (-2,-3) = (3,-6)
=(5,-3) - (-2,-3) = (7,0)
Setting the x-coordinates equal gives the equation -12k = 4.
Setting the y-coordinates equal gives the equation -9k = 3.
Both of these have the same solution: ![]() . So this is the solution.
. So this is the solution.
Setting the x-coordinates equal gives the equation 8k = 4. This has the solution ![]() .
.
Setting the y-coordinates equal gives the equation 7k = 3. This has the solution ![]() .
.
Since these solutions are different, the original equation has no solution.
![]() . We call this point A.
. We call this point A.
When t= 0 the person is at (2,0). We call this point B.
Our method: We define D = B - A. Thus, D= (2,0) - ![]() =
= ![]() .
.
So, the person's position at time t is A + tD = ![]() + t
+ t![]() . Here is the sketch:
. Here is the sketch:
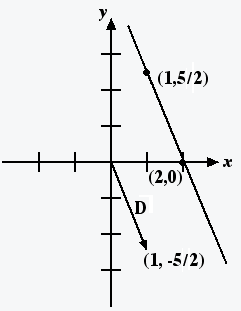
![]() .
This line is shown in red in the sketch.
(Please ignore the blue for a moment ... )
.
This line is shown in red in the sketch.
(Please ignore the blue for a moment ... )
![]() . This line is shown in green in the sketch.
. This line is shown in green in the sketch.
![]() .
This turns out to be same line as in part i.
So, we have (lightly) re-sketched this line in blue.
.
This turns out to be same line as in part i.
So, we have (lightly) re-sketched this line in blue.
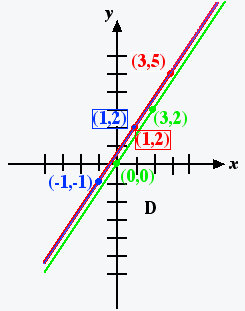
Note: This is not the only possible correct solution. We could have chosen a different starting point and/or a different second point. But in any correct solution, the direction vector will proportional to (1,-1).
![]() . So, we'll work with x= 0 and x=7 to minimize the messiness of the fractions. So, x= 0 gives the point
. So, we'll work with x= 0 and x=7 to minimize the messiness of the fractions. So, x= 0 gives the point ![]() , while x= 7 gives the point
, while x= 7 gives the point ![]() .
.
Thus, D = B - A = ![]() = (7,5). This leads to the parametric form
= (7,5). This leads to the parametric form ![]() .
.
The parametric forms of points on the two lines
are as follows:
(1,1) + s(4,-2) = (1 + 4s, 1 - 2s),
and
(0,3) + t(3,0) = (3t, 3).
So, we set the x-coordinate on one line equal to the x-coordinate
on the other line, and similarly for the y-coordinates.
In this way,
we get the following system of equations:
1 + 4s = 3t
1 - 2t = 3.
The second equation simplifies to -2t = 2, thus yielding the
solution t = -1.
If we sbstitute this into the first equation, it becomes
1 + 4s = -3.
We can simplify this to 4s = -4, thus obtaining the solution
s = -1.
If we substitute s = -1 into the parametric description
of the first line, we find the point (-3,3),
and similarly, if we substitute t = -1 into the parametric
description of the second line, we find the point (-3,3).
So, the point of intersection is (-3,3).
Note: We can find the answer by doing just one of
these last two substitutions,
but by doing both we can check our answer.
The parametric forms of points on the two lines
are as follows:
(4,4) + r(2,1) = (4 + 2r, 1 + r),
and
(0,0) + s(-6,-3) = (-6s, -3s).
So, we set the x-coordinate on one line equal to the x-coordinate
on the other line, and similarly for the y-coordinates.
In this way,
we get the following system of equations:
4 + 2r = -6s
1 + r = -3s
We can re-arrange this as follows:
2r + 6s = -4
r + 3s = -1.
We can transform this system by multiplying the second equation
by -2 and adding it to the first equation.
If we do this,
then our system of equations becomes:
r + 3s = -1
0 = -2.
But this last result is self-contradictory. So, there is
no solutions, and the two lines
do not intersect.
Thus, the two lines are parallel, as you can see by drawing a sketch.
(To do that, note that the slope = 1/ 2.)
The parametric forms of points on the two lines
are as follows:
(3,-1) + s(-2,-5) = (3 - 2s, -1 - 5s),
and
(5,4) + t(4,10) = (5 + 4t, 4 + 10t).
(A misprint in the problem has been corrected here.)
So, we set the x-coordinate on one line equal to the x-coordinate
on the other line, and similarly for the y-coordinates.
In this way,
we get the following system of equations:
3 - 2s = 5 + 4t
-1 - 5s = 4 + 10t
We can re-arrange this as follows:
-2s + 4t = 2
-5s + 10t = 5.
We can transform this system by multiplying the second equation
by 5/ 2 and adding it to the first equation.
If we do this,
then our system of equations becomes:
-2s + 4t = 2
0 = 0
This time we can always find a value for s,
no matter what value is chosen for t.
Thus, the system has infinitely many solutions, and the
"two" lines are actually identical.
As in part ii,
you can check this by making a sketch.
Q - P = (c,d) - (a,b) = (c-a, d-b).
We substitute these last coordinates into the definition of the norm, and here's what we find:
||Q - P|| = ((c-a)2 + (d-b)2)1/2.
(approximate numerical value = 9.22).
(approximate numerical value = 6.32).
In other words, the norm of the sum of two vectors need not be equal to sum of the two norms. If we think of A and B as representing points of the plane, then can draw the line segment joining the origin to A and the segment joining the origin to B. Then the real numbers ||A|| and ||B|| are just the lengths of these two segments. But by similar reasoning (admittedly a bit more involved), the norm of the sum is going to be the length of the diagonal of the parallelogram. And there certainly is no reason to expect the length of the diagonal to equal to the sum of the lengths of two of the sides of the parallelogram.
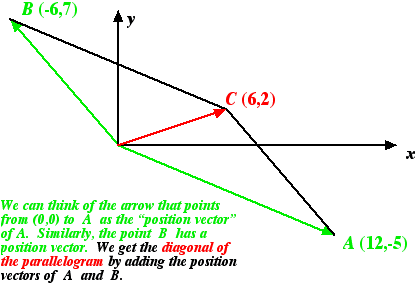
P(3) - P(0) = (-3,32) - (9,11) = (-12, 21).
(Of course, we know that real life usually isn't
this simple!)
![]() = np =
= np = ![]() = 30.
= 30.![]() =
= ![]() =
= ![]() = 5.
= 5.
Here, q = 1 - p, by definition.
![]() =
= ![]() =
= ![]() = 0.1.
= 0.1.![]() =
= ![]() = 0.1.
= 0.1.
![]() , where p =
, where p = ![]() and q = 1 - p =
and q = 1 - p = ![]() .
.![]()
![]()
![]()
![]()
![]() =
= ![]() =
= ![]() = 0.79558.
= 0.79558.
![]() = np.
= np.
Since we know that p = 0.9, but we don't know how many tickets are to be sold,
we have ![]() = .9n.
= .9n.
![]() =
= ![]()
The part to the left of the mid-line is 50% of the area under the curve (by symmetry). Hence the part of the shaded area
which is to the right of the mid-line is 80% - 50% = 30%. So, we want to have A(z) = .3. The two closest values
in Table 11.6 are A(z) = .2881, corresponding to z = .8, and A(z) = .3159, corresponding to z = .3159.
The closer of the two is z = .8, although we also could choose to split the difference and take z = .85.
![]() + zs = 250 to find the value of n. Substituting the values of
+ zs = 250 to find the value of n. Substituting the values of ![]() and s from exercise 11.5.7,
and s from exercise 11.5.7,
and the value of z from exercise 11.5.8, we get the following:![]() = 250.
= 250.![]() = 250 - .9n
= 250 - .9n
![]() )2 = (250 - .9n)2, or:
)2 = (250 - .9n)2, or:
.7225·.09n = 2502 - 2·250·.9n + .81n2
![]()
= ![]()
= ![]()
![]() = .09· 273.09 = 245.78,
= .09· 273.09 = 245.78,
and zs = .85·![]() = 4.21.
= 4.21.![]() + zs = 250.
+ zs = 250.