Ellipsoid
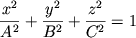
|
|
Just as an ellipse is a generalization of a circle, an ellipsoid is a generalization of a sphere. In fact, our planet Earth is not a true sphere; it's an ellipsoid, because it's a little wider than it is tall. As you can verify to the left, all of the cross sections of an ellipsoid are ellipses. The picture shows an ellipsoid where A=3, B=2, and C=1. Looking at the graph, this gives you a hint about how the constants affect the surface. An ellipsoid centered at the origin stretches out A units in the positive and negative x direction; B units in the positive and negative y direction; and C units in the positive and negative z direction. What this means is that an ellipsoid is probably the easiest quadric surface to draw accurately. (Or, if your drawing skills are like mine, you at least know what it should look like, even if the actual drawing is somewhat lacking!) You can interactively adjust the values of A, B, and C in the second picture. Notice that you can get everything from a sphere to a nearly flat pancake. Here are some things which deserve a little thought on your part:
|





