Hyperbolic Paraboloid
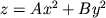
(where A and B have DIFFERENT signs)
|
Display Gridlines: |
With just the flip of a sign, say we can change from an elliptic paraboloid to a much more complex surface. Because it's such a neat surface, with a fairly simple equation, we use it over and over in examples. Hyperbolic paraboloids are often referred to as "saddles," for fairly obvious reasons. Their official name stems from the fact that their vertical cross sections are parabolas, while the horizontal cross sections are hyperbolas. But even the vertical cross sections are more complicated than with an elliptic paraboloid. Look at the picture on the left, which shows the surface z = x2 - y2. Notice that the parabolas open in different directions; the green parabolas open downward, while the purple ones open upward. Also, the hyperbolas which make up the horizontal cross sections can open in either the x- or y- direction, depending on the chosen value for z. All of these are important features of any hyperbolic paraboloid. The second picture lets you explore what happens when you adjust the coefficients of the equation (Here we're assuming A is positive and B is negative; in other words this "looks" like z = x2 - y2.) Here are a few things for you to think about:
Be very careful; if you hear somebody refer simply to a "paraboloid," they generally mean an elliptic paraboloid, or even a surface where A=0 or B=0. If you're in doubt which surface somebody means, ask. |





